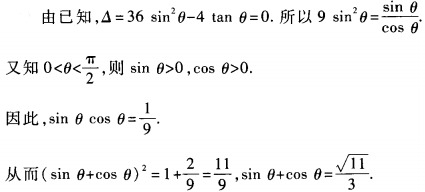单选题
1、在△ABC中,若b= ,c=
,c=
 则a等于()
则a等于()
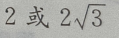
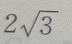
答 案:B
解 析:此题是已知两边和其中一边的对角,解三角形时,会出现一解、两解、无解的情况,要注意这一点.用余弦定理 可得
可得

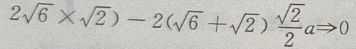
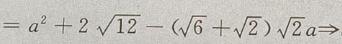
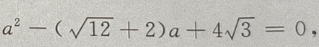 解出
解出


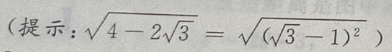
2、一批产品共有5件,其中4件为正品,1件为次品,从中一次取出2件均为正品的概率为()。
答 案:A
解 析:本题主要考查的知识点为随机事件的概率
一次取出2件均为正品的概率为
3、如果球的大圆面积增为原来的4倍,则该球的体积就增为原来的()。
答 案:B
解 析:
4、两条直线是异面直线的充分条件是这两条直线()。
答 案:D
主观题
1、已知抛物线C:y2=2px(p>0)的焦点到准线的距离为1。 (I)求C的方程; (Ⅱ)若A(1,m)(m>0)为C上一点,O为坐标原点,求C上另一点B的坐标,使得OA⊥OB
答 案:(I)由题意,该抛物线的焦点到准线的距离为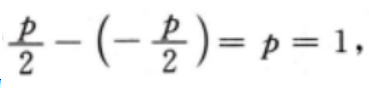 所以抛物线C的方程为
所以抛物线C的方程为 (Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得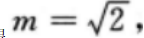 因此A点坐标为
因此A点坐标为 设B点坐标为
设B点坐标为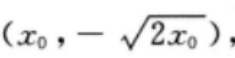 则
则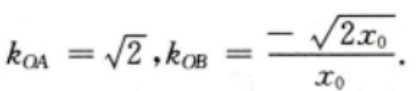 因为
因为 则有
则有 即
即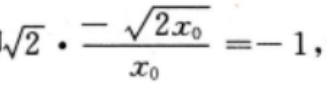 解得x0=4
所以B点的坐标为
解得x0=4
所以B点的坐标为
2、在正四棱柱ABCD-A'B'C'D'中, (Ⅰ)写出向量
(Ⅰ)写出向量 关于基底{a,b,c}的分解式
(Ⅱ)求证:
关于基底{a,b,c}的分解式
(Ⅱ)求证: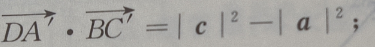 (Ⅲ)求证:
(Ⅲ)求证: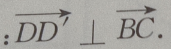
答 案:(Ⅰ)由题意知(如图所示) 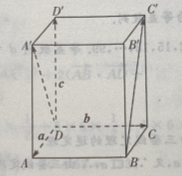
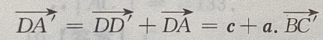
 (Ⅱ)
(Ⅱ)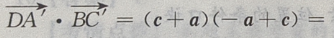
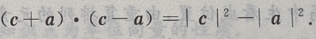 (Ⅲ)
(Ⅲ)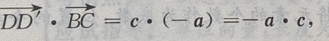 由已知,a,c是正四棱柱的棱,a,b,c两两垂直
由已知,a,c是正四棱柱的棱,a,b,c两两垂直

3、设A1A2A3A4A5A6为正六边形,如图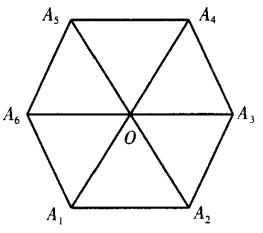 ,O为它的中心。 (1)求证:
,O为它的中心。 (1)求证: 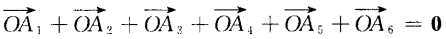 (2)
(2)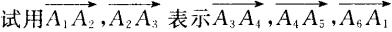
答 案:已知A1A2A3A4A5A6 为正六边形,即|A1A2|=|A3A4|=......|A6A1|.要证6个向量的和为0.只需证其中3个向量与另3个向量的长度相等、方向相反即可.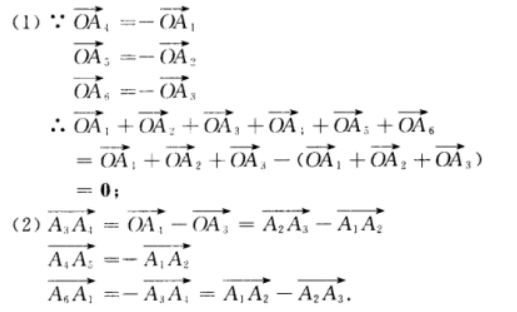
4、已知a,b,c成等差数列,a,b,c+1成等比数列.若b=6,求a和c.
答 案:由已知得 解得
解得
填空题
1、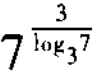 =______。
=______。
答 案:27
解 析: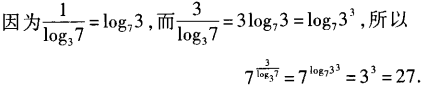
2、已知关于t的二次方程t2-6tsinθ+tanθ=0(0<θ<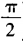 )的两根相等,则sinθ+cosθ的值等于______。
)的两根相等,则sinθ+cosθ的值等于______。
答 案: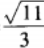
解 析: