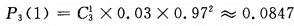单选题

1、下列函数中，为偶函数的是（）。

• A：
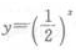
• B：
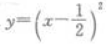
• C：
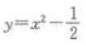
• D：

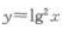
答 案：C

解 析：根据函数的奇偶性的定义可知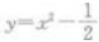为偶函数

2、直线l1与l2：3x + 2y - 12 =0 的交点在x轴上，且l1⊥l2，则l1在y轴的截距是（）。

• A：-4
• B：
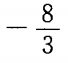
• C：4
• D：

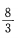
答 案：B

解 析：

3、设函数f(x)＝e^x，则f(x－a)·f(x＋a)＝（）。

• A：f(x²－a²)
• B：2f(x)
• C：f(x²)
• D：f²(x)

答 案：D

4、设集合M＝{0，1，2，3，4}，N＝{1，2，3}，T＝{2，4，6}，则集合（M∩T）∪N＝（）。  

• A：{0，1，2，3，4，6}
• B：{1，2，3，4}
• C：{2，4}
• D：{2，4，6}

答 案：B

解 析：M∩T＝（2，4），则集合（M∩T）∪N＝{1，2，3，4}。答案为B。  

主观题

1、记△ABC的内角A，B，C的对边分别为a，b，c，已知B=60°，b²=ac，求A。    

答 案：由余弦定理b²=a²+c²-2accosB，可得ac=a²+c²-ac，即a²+c²-2ac=(a-c)²=0，解得a=c。 又因为B=60°，故△ABC为等边三角形，所以A=60°

2、已知函数f(x)=(x-4)(x²-a) （I）求f"(x)； (Ⅱ)若f"(-1)=8，求f(x)在区间[0，4]的最大值与最小值

答 案：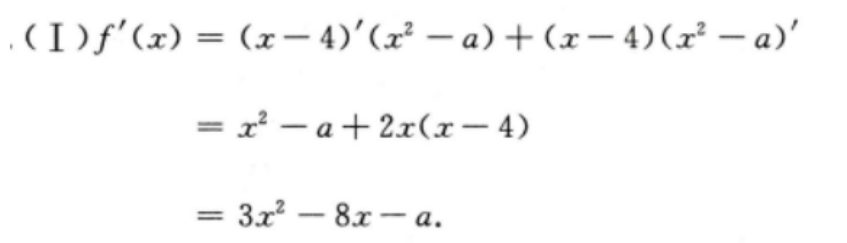

3、如图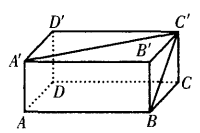，已知长方体的长和宽都是4cm，高是2cm。求 （1）BC和A’C’所成的角是多少度?
（2）A’B’和DD’的距离是多少?

答 案：（1）在长方体中BC和A’C’不在同一个平面内 所以BC和A’C’是异面直线 ∵在长方体中BC//B’C’ ∴∠A’C’B’是异面直线BC和A’C’所成的角
∵A’C’B’=45°
异面直线BC和A’C’所成的角是45°
（2）A’B’和DD’是异面直线
∵A’D’⊥A’B’ A’D’⊥DD’
∴A’D’的长即为异面直线A’B’和DD’的距离
∵A’D’=4
∴A’B’和DD’间的距离为4cm。

4、设函数f(x)=xlnx+x.(I）求曲线y=f(x）在点（(1,f(1))处的切线方程；
(II）求f（x）的极值．

答 案：(I）f(1)=1,f'(x)=2+lnx，故f'(1)=2.所以曲线y=f(x）在点（1,f(1))处的切线方程为y=2x-1.(II）令f'(x)=0，解得当时，f'(x)时，f'(x)＞O.故f(x）在区间单调递减，在区间单调递增．因此f(x）在时取得极小值

填空题

1、在自然数1、2、…、100中任取一个数，该数能被3整除的概率是______。  

答 案：0.33

解 析：此题随机试验包含的基本事件总数n=100，且每个数能被取到的机会均等，即属于等可能事件的概率能被3整除的自然数的个数m=33，故所求概率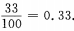  

2、100件产品中有3件次品，每次抽取一件，有放回的抽取三次，恰有1件是次品的概率是______。  

答 案：0.0847

解 析：由于三次抽取是独立的，每次抽取可看做是一次试验，每次试验只有两个可能结果：“正品”或“次品”，次品率为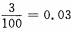，因此二次独立且重复试验恰有1件次品率为