2025年成考专升本《高等数学一》每日一练试题01月02日
精选习题
2025-01-02
11:43:20
收藏
单选题
1、下列等式成立的是()。
- A:
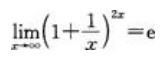
- B:
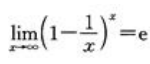
- C:
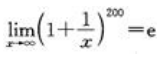
- D:
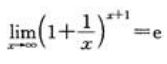
答 案:D
解 析:A项,由 ,可知
,可知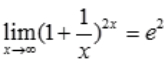 ;B项,
;B项, ;C项,
;C项,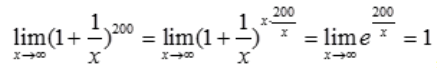 ;D项,
;D项, 。
。
2、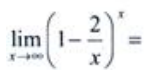 ()。
()。
- A:
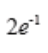
- B:
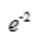
- C:
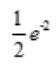
- D:
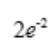
答 案:B
解 析:根据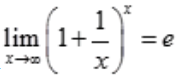 ,可得
,可得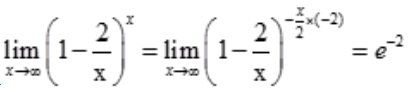 。
。
3、 ()。
()。
- A:>0
- B:<0
- C:=0
- D:不存在
答 案:C
解 析:被积函数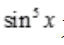 为奇函数,且积分区间[1,1]为对称区间,由定积分的对称性质知该函数的积分为0。
为奇函数,且积分区间[1,1]为对称区间,由定积分的对称性质知该函数的积分为0。
主观题
1、求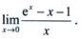
答 案:解:利用洛必达法则,得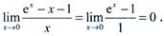
2、求微分方程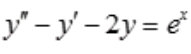 的通解。
的通解。
答 案:解:对应的齐次方程为 。特征方程
。特征方程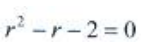 ,特征根
,特征根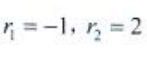 齐次方程通解为
齐次方程通解为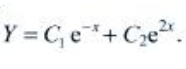 原方程特解为
原方程特解为 ,代入原方程可得
,代入原方程可得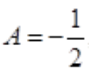 ,因此
,因此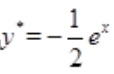 。
。
方程通解为
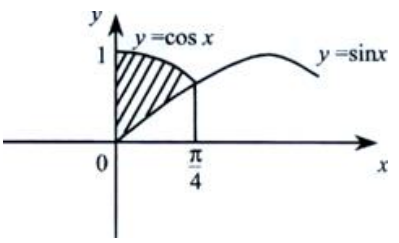
3、求曲线y=sinx、y=cosx、直线x=0在第一象限所围图形的面积A及该图形绕x轴旋转一周所得旋转体的体积Vx。
答 案:解:由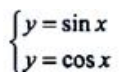 ,解得两曲线交点的x坐标为
,解得两曲线交点的x坐标为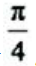 。
。
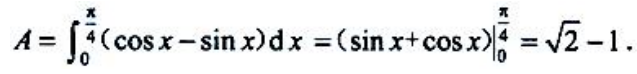

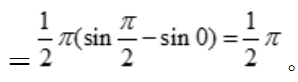
填空题
1、设F(x,y,z)=0,其中z为x,y的二元函数,F(x,y,z)对x,y,z存在连续偏导数,且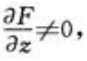 则
则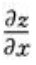 =()。
=()。
答 案: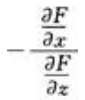
解 析:根据复合函数求偏导法则可得: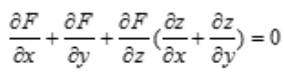 ,要求z对x的偏导,则把y看做常数,所以有
,要求z对x的偏导,则把y看做常数,所以有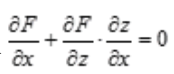 ,所以
,所以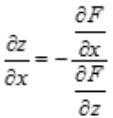 。
。
2、设z=xy,则dz=()。
答 案:ydx+xdy
解 析:z=xy,则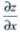 =y,
=y,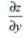 =x.由于dz=
=x.由于dz=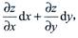 可知dz=ydx+xdy。
可知dz=ydx+xdy。
3、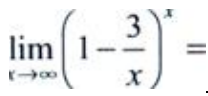 ()。
()。
答 案:e-3
解 析:所给极限为重要极限的形式,由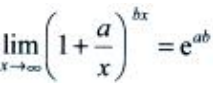 ,可得
,可得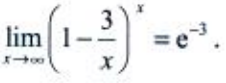
简答题
1、
答 案:
更多推荐

