单选题

1、已知集合

• A：
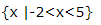
• B：
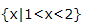
• C：
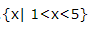
• D：

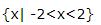
答 案：B

解 析：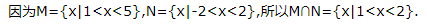

2、在等差数列{a_n}中，S_n为数列{a_n}的前n项和，若S₂=0,S₄=8,则a₆=（）

• A：5
• B：7
• C：9
• D：16

答 案：C

解 析：

3、已知两个非零向量a和b满足a·b=0,则a与b的夹角为()

• A：180°
• B：90°
• C：45°
• D：0°

答 案：B

解 析：设向量a,b的夹角为α,α∈[0°,180°].因为向量a,b是非零向量，所以|a|≠0,|b|≠0.由a·b=|a|·|b|cosα=0可得cosα=0,故α=90°,即向量a,b的夹角为90°.

4、直线x+y-1=0与直线x+y+1=0的位置天系是（）  

• A：垂直
• B：平行
• C：相交
• D：重合

答 案：B

解 析：易知直线x+y-1=0,即y=-x+1的斜率为-1,在y轴上的截距为1,直线x+y+1=0,即y=-x-1 的斜率为 -1,在y轴上的截距为 -1.因为两直线的斜率相等,在y轴上截距不相等,所以两直线的位置关系是平行.

填空题

1、7 个人站成一排,如果甲、乙2人必须站在两端,有（）种排法.  

答 案：240

解 析：第一步,先排甲和乙,有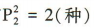排法;第二步,将剩下的5人排成一排,有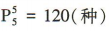排法.根据分步计数原理知,共有2x120=240(种)排法.

2、已知角α的顶点与坐标原点重合，始边与x轴正半轴重合，终边经过点P(x,-3),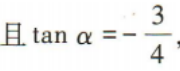 sinα的值为（）

答 案：

解 析：

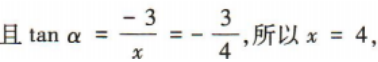
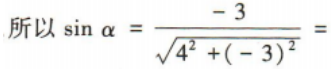
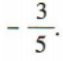
3、以点(2,1)为圆心,且与直线4x-3y=0相切的圆的标准方程为（）  

答 案：(x-2)²+(y-1)²=1

解 析：圆心(2,1)到切线4x-3y=0的距离为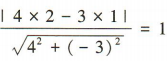,所以所求圆的标准方程为(x-2)²+(y-1)²=1.

4、若(x-1)ⁿ的展开式中x²的系数是-10,则n的值为()  

答 案：5

解 析：因为(x-1)ⁿ的展开式中x²的系数是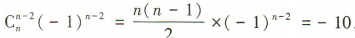,所以n= 5.

简答题

1、记Sn为等差数列{an}的前n项和，已知a1=-9,S3=-21. (1)求{an}的通项公式； (2)求Sn的最小值及取得最小值时n的值.

答 案：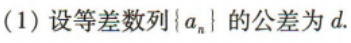

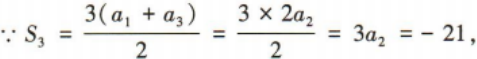
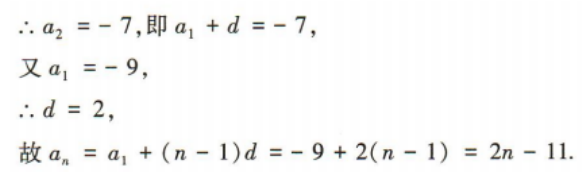
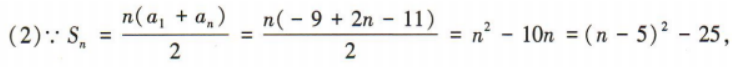
2、如图所示，某学校要建矩形运动场地，场地相邻两边借用两面墙，另两条边的长度之和为16m,设矩形的长为x m.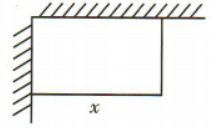 (1)求矩形运动场地面积S关于x的函数关系式，并指出函数的定义域；(2)当x为何值时，场地面积S最大?最大面积是多少?

答 案：(1)因为矩形的长为x m,长与宽的和为16m, 所以矩形的宽为(16-x)m. 所以S=x(16-x). 所以S=x(16-x)的定义域为[8,16). (2)S=x(16-x)=16x-x²=-(x-8)²+64,图像开口向下， 所以S=x(16-x),x∈[8,16)在[8,16)上单调递减， 所以当x=8时，场地面积S最大，最大面积为64m²