2024年成考专升本《高等数学二》每日一练试题12月19日
精选习题
2024-12-19
11:28:15
收藏
判断题
1、若
，则
。（）
答 案：错
解 析：
所以
单选题
1、
（）.
- A：0
- B：
- C：1
- D：e
答 案：B
解 析：因为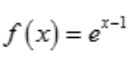
是初等函数，在定义区间（x∈R）内是连续的，其极限值等于函数值，所以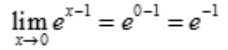
2、已知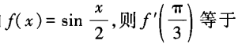
（）。
- A：
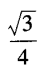
- B：
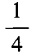
- C：
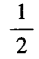
- D：
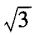
答 案：A
解 析：先用复合函数求导公式计算出f’（x），再将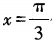
代入。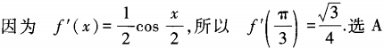 
。
主观题
1、计算
．
答 案：解：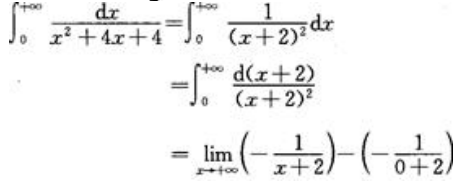
．
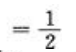2、求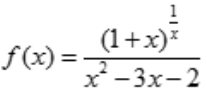
的间断点，并指出类型．
答 案：解：因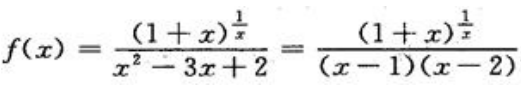
，故x＝0，x＝1，x＝2是f（x）的间断点，又
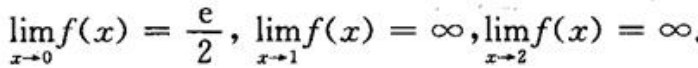又因，f（0）、f（1）、f（2）都不存在，所以x＝0是f（x）的第一类间断点（可去间断点）；x＝1，x＝2是，f（x）的第二类间断点（无穷间断点）．
填空题
1、
=()
答 案：
解 析：
2、设
，则
（）
答 案：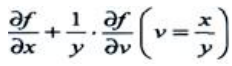
解 析：设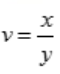
，则z＝f（x，v），则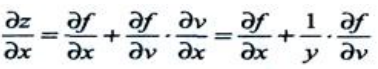
简答题
1、设y=x2·ex，求y’。
答 案：本题考查的知识点是函数乘积的导数计算。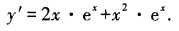 
2、设z=z（x，y）是由方程x2+y2+z2=ez所确定的隐函数，求dz。
答 案：
更多推荐
