2024年成考高起点《数学(理)》每日一练试题12月10日
精选习题
2024-12-10
12:25:05
收藏
单选题
1、设log2x=a,则log2(2x2)=()。
- A:2a2+1
- B:2a2-1
- C:2a-1
- D:2a+1
答 案:D
解 析:本题主要考查的知识点为对数函数的性质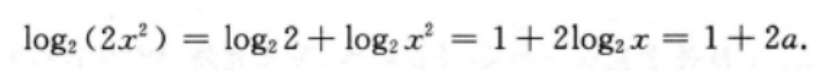
2、下列函数中为奇函数的是()。
- A:y=2lgx
- B:y=3x+3-x
- C:y=x3+sin2x
- D:y=x3+tanx
答 案:D
解 析:对于D,f(-x)=(-x)3+tan(-x)=-(x3+tanx)=-f(x)。答案为D。
3、对满足a>b的任意两个非零实数,下列不等式成立的是()
- A:
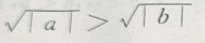
- B:
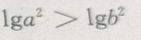
- C:

- D:
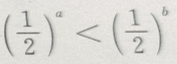
答 案:D
解 析:A错误,例如-2>4,而 B错误,例如:-10>100,而
B错误,例如:-10>100,而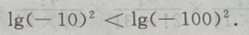 C错误,例如:-1>-2,而
C错误,例如:-1>-2,而
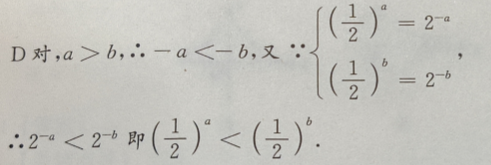
4、两个数的等差中项为20,等比中项为12,那么这两个数为()。
- A:18,22
- B:9,16
- C:4,36
- D:16,24
答 案:C
主观题
1、求(1+tan10°)(1+tan35°)的值。
答 案:原式=1+tan10°+tan35°+tan10°·tan35°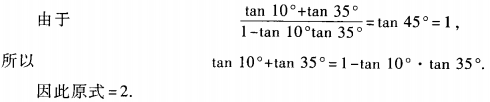
2、在△ABC中如果sinA=2sinBcosC,求证:△ABC是等腰三角形。
答 案: ∴△ABC为等腰三角形。
∴△ABC为等腰三角形。
3、已知抛物线C:y2=2px(p>0)的焦点到准线的距离为1。 (I)求C的方程; (Ⅱ)若A(1,m)(m>0)为C上一点,O为坐标原点,求C上另一点B的坐标,使得OA⊥OB
答 案:(I)由题意,该抛物线的焦点到准线的距离为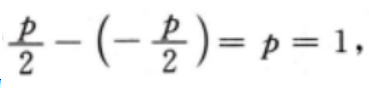 所以抛物线C的方程为
所以抛物线C的方程为 (Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得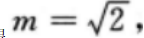 因此A点坐标为
因此A点坐标为 设B点坐标为
设B点坐标为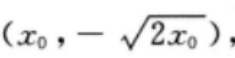 则
则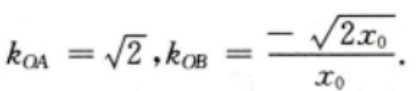 因为
因为 则有
则有 即
即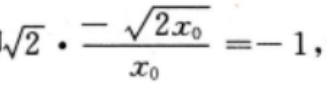 解得x0=4
所以B点的坐标为
解得x0=4
所以B点的坐标为
4、已知等差数列前n项和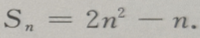 (Ⅰ)求这个数列的通项公式;(Ⅱ)求数列第六项到第十项的和
(Ⅰ)求这个数列的通项公式;(Ⅱ)求数列第六项到第十项的和
答 案: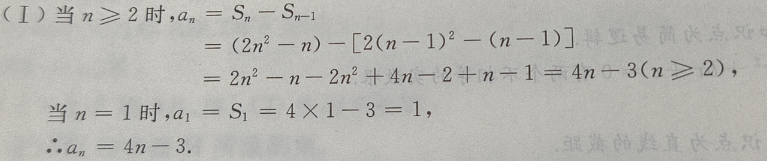

填空题
1、在△ABC中,a=2,b=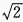 ,∠B=
,∠B=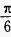 ,则∠A=______。
,则∠A=______。
答 案:
解 析: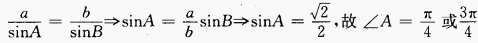
2、过点(2,0)作圆x2+y2=1的切线,切点的横坐标为()。
答 案: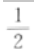
解 析:本题主要考查的知识点为圆的切线.
设切点(x0,y0)则有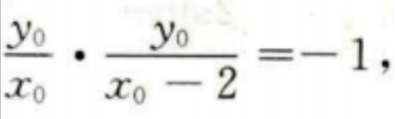 即
即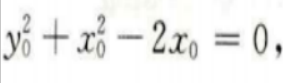
 所以
所以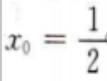 故切点横坐标为
故切点横坐标为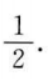
更多推荐

