判断题

1、y=-x³是偶函数。（）  

答 案：错

解 析：f（-x）=f（x）是偶函数的定义。由题意可知，f（-x）=-f（x），所以应该是奇函数。

2、二项式（x+1）⁵的展开式共6项。（）  

答 案：对

解 析：n次方的展开式有n+1项，5次方的展开式有6项

单选题

1、如图，在三棱锥P-ABC中，平面PAB⊥平面ABC，PA=PB=AB=2，AB⊥BC，BC=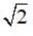，则直线PC与平面ABC所成的角是（）  

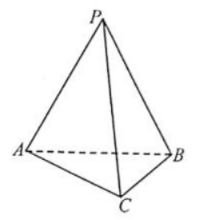
• A：30°
• B：45°
• C：60°
• D：90°

答 案：B

2、已知,函数f(x)=x(1-x)的最大值是().

• A：
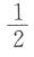
• B：
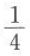
• C：
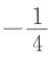
• D：无最大值

答 案：B

解 析：本题主要考查求二次函数在闭区间上的最值，二次函数的性质的应用。

多选题

1、下列四个命题中正确的是（）  

• A：与圆有公共点的直线是该圆的切线
• B：垂直于圆的半径的直线是该圆的切线
• C：到圆心的距离等于半径的直线是该圆的切线
• D：过圆直径的端点，垂直于此直径的直线是该圆的切线

答 案：CD

解 析：A中，与圆有两个公共点的直线，是圆的割线，故该选项不符合题意；B中，应经过此半径的外端，故该选项不符合题意；C中，根据切线的判定方法，故该选项符合题意；D中，根据切线的判定方法，故该选项符合题意。故选：CD。

2、下列命题中，不正确的是（）  

• A：三点可确定一个圆
• B：三角形的外心是三角形三边中线的交点
• C：一个三角形有且只有一个外接圆
• D：三角形的外心必在三角形的内部或外部

答 案：ABD

解 析：A、不在同一条直线上的三点确定一个圆，故本选项错误；B.、三角形的外心是三角形三边垂直平分线的交点，所以本选项是错误；C、三角形的外接圆是三条垂直平分线的交点，有且只有一个交点，所以任意三角形一定有一个外接圆，并且只有一个外接圆，所以本选项是正确的；D、直角三角形的外心在斜边中点处，故本选项错误。故选：ABD

主观题

1、已知函数f(x)=log₃(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.

答 案：(1)根据题意可得，3x-1>0,解得所以函数f(x)的定义域是(2)因为f(x)=log₃(3x-1)<1=log₃3,f(x)为定义域上的增函数，所以O<3x-1<3,解得所以x的取值范围是

2、已知等差数列{an}的前n项和S_n且S₅=35,S₈=104.
(1)求数列{an}的通项公式；
(2)若{b_n}为等比数列，b₁=a₂,b₂=a₃+2,求数列{b,}的公比q及前n项和T_n.

答 案：(1)所以a₆=19.则数列{an}的公差，通项公式为an=a₆+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以则

填空题

1、某地一抛物线形拱桥，当水面离桥顶2m时，水面宽4m,若水面下降1m,则水面宽为（）m.  

答 案：

解 析：建立适当的直角坐标系，设抛物线方程为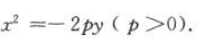.由题意可知，抛物线过点(2,-2),所以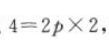,解得p=1,所以抛物线方程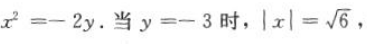为水面宽为

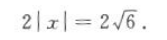
2、若集合A={9,1,a-1},B={-2,a²},B为A的子集，则a的值是（）。

答 案：-1

解 析：由题意可知a-1=-2,解得a=-1,所以a²=1,所以N={-2,1}。