单选题

1、过点A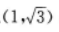与圆x²+y²=1相切的直线方程是（）

• A：
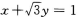
• B：
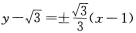
• C：
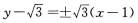
• D：以上都不是

答 案：D

解 析：【考点指要】本题主要考查的内容是利用点到直线的距离公式求直线的斜率，从而写出所求的直线方程，这是考试大纲要求掌握的概念．从近几年的试题分析可知，这类题的深度在今后成人高考中有可能加大，希望考生予以足够的重视．

2、已知x+x^-1=2cos40°，则x⁴+x^-4=（）。

• A：2cos20°
• B：-2cos20°
• C：2sin80°
• D：-2sin80°

答 案：B

解 析：由已知得(x+x^-1)²=(2 cos 40°)²,x²+2+x^-2=4cos²40° x²+x^-2=2(2 cos²40°-1)= 2cos 80°同样可得x⁴+x^-4=2 cos 160°=-2 cos 20°故选B。

3、已知sinα=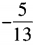，且540°＜α＜630°，则sin2α=（）。

• A：
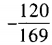
• B：
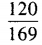
• C：
• D：

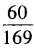
答 案：B

解 析：由已知，360°+180°＜α＜360°+270°，所以α是第三象限的角，故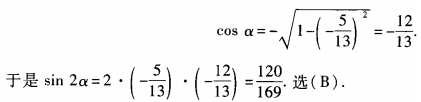

4、设甲：四边形ABCD是平行四边形，乙：四边形ABCD是正方形，则（）。

• A：甲是乙的充分条件，但不是乙的必要条件
• B：甲是乙的必要条件，但不是乙的充分条件
• C：甲是乙的充分必要条件
• D：甲不是乙的充分条件，也不是乙的必要条件

答 案：B

主观题

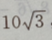1、已知三角形的一个内角是，面积是周长是20,求各边的长.  

答 案：设三角形三边分别为a,b,c,∠A=60°，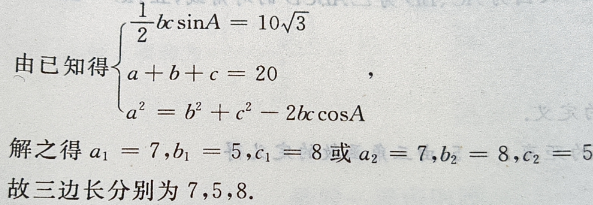  

2、求下列函数的最大值、最小值和最小正周期： （1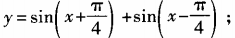） 2）y=6cosx+8sinx

答 案： 所以函数的最大值是最小值是最小正周期为2π， （2）要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式，需使cosx与sinx的系数平方和为1，为此，将已知函数化为 因此,函数的最大值是10,最小值是-10,最小正周期为2π

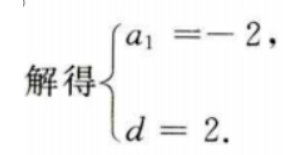
3、已知等差数列{an}中，a1+a3+a5=6，a2+a4+a6=12，求{an}的首项与公差.  

答 案：因为{an}为等差数列，则

4、设椭圆的中心是坐标原点，长袖在x轴上，离心率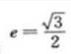，已知点P（0,3/2）到椭圆上的点的最远距离是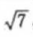，求椭圆的方程。

答 案：

填空题

1、某学科的一次练习中，第一小组5个人成绩如下(单位：分)：98，89，70，92，90，则分数的样本方差为__________．

答 案：88．96

解 析：平均分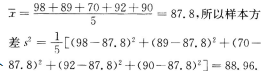 【考点指要】本题主要考查样本的平均数与方差的计算．对于统计问题，只需记清概念和公式，计算时不出错即可．  

2、过点（2，0）作圆x2+y2=1的切线，切点的横坐标为（）。

答 案：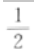

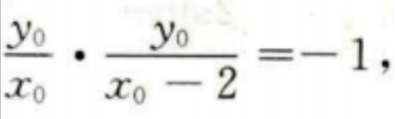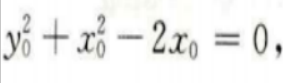
解 析：本题主要考查的知识点为圆的切线. 设切点(x0,y0)则有 即所以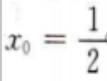故切点横坐标为