判断题

1、若2,x,8成等比数列，则x=±4。（）  

答 案：对

2、函数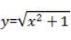的定义域为全体实数。（）  

答 案：对

单选题

1、点（-sin30°，cos30°）关于y轴对称的点的坐标是（）  

• A：(1/2,)
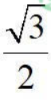• B：(1/2,)
• C：(-1/2,)
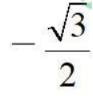• D：(-1/2,)

答 案：A

2、如图，平面上直线a,b分别过线段OK两端点（数据如图)，则a，b相交所成的锐角是()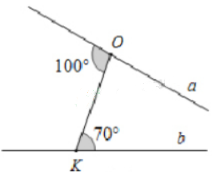  

• A：20°
• B：30°
• C：70°
• D：80°

答 案：B

解 析：a，b相交后，与OK组成了一个三角形，根据三角形的外角的性质列式计算即可得解。根据图形可知，a，b相交所成的锐角=100°-70°=30°。故选B

多选题

1、已知数列{3n-1}，下面选项正确的是（）  

• A：这个数列是公比为3的等比数列
• B：这个数列是公差为3的等差数列
• C：这个数列的第5项是14
• D：20是这个数列的第7项

答 案：BCD

解 析：已知数列{3n-1}，这个数列是公差为3的等差数列，故A错误，B正确。数列第五项=3*5-1=14。故C正确。数列第七项=3*7-1=20.故D正确

2、下列计算结果正确的是（）  

• A：
• B：
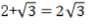
• C：
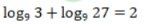
• D：

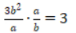
答 案：AC

主观题

1、已知两直线,当m为何值时，l₁与l₂: (1)相交；(2)平行；(3)重合.  

答 案：(1)当1×3m-(m-2)m²=-m²(m-2)+3m=-m(m-3)(m+1)≠0时，l₁与l₂相交，即m≠0,m≠3且m≠-1. (2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时，l₁与l₂平行，即m=0或m=-1. (3)当-m(m-3)(m+1)=0且12-4m=0时，l₁与l₂重合，即m=3.

2、已知等差数列{an}的前n项和S_n且S₅=35,S₈=104.
(1)求数列{an}的通项公式；
(2)若{b_n}为等比数列，b₁=a₂,b₂=a₃+2,求数列{b,}的公比q及前n项和T_n.

答 案：(1)所以a₆=19.则数列{an}的公差，通项公式为an=a₆+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以则

填空题

1、设4cos x=a,那么a的取值范围是（）.

答 案：[-4,4]

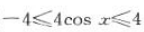解 析：因为,所以,则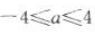,即a的取值范围是[-4,4].

2、设集合,,则AUB=（）.

答 案：[-3,4)

解 析：因为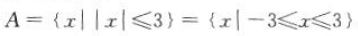集合,集合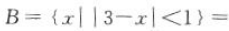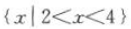,所以AUB=[-3,4).