判断题

1、方程x²-2x+3=0没有实根。（）  

答 案：对

2、函数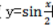的最小正周期是。（）  

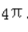答 案：对

解 析：y=sin(x/2+π/3)最小正周期是：2π/(1/2)=4π

单选题

1、某小组有成员3人，每人在一个星期中参加1天劳动，如果劳动日期可随机安排，则3人在不同的3天参加劳动的概率为（）

• A：
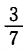
• B：
• C：
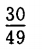
• D：

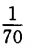
答 案：C

解 析：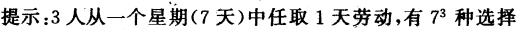

2、已知数列{a_n}的前n项和为S_n=5n²−n,则a₆+a₇+a₈+a₉+a₁₀等于()

• A： 250
• B： 270
• C： 370
• D： 490

答 案：C

多选题

1、已知等差数列{a_n}的前n项和为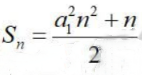，公差为d，则（）  

• A：a₁=1
• B：d=1
• C：2S_n-a_n=1+3+5+...+(2n-1)
• D：

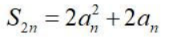
答 案：ABC

2、已知点P到圆O上的点的最大距离是7cm，最小距离是1m，则圆O的半径是（）  

• A：4cm
• B：3cm
• C：5cm
• D：6cm

答 案：AB

主观题

1、已知函数f(x)=log₃(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.

答 案：(1)根据题意可得，3x-1>0,解得所以函数f(x)的定义域是(2)因为f(x)=log₃(3x-1)<1=log₃3,f(x)为定义域上的增函数，所以O<3x-1<3,解得所以x的取值范围是

2、已知两直线,当m为何值时，l₁与l₂: (1)相交；(2)平行；(3)重合.  

答 案：(1)当1×3m-(m-2)m²=-m²(m-2)+3m=-m(m-3)(m+1)≠0时，l₁与l₂相交，即m≠0,m≠3且m≠-1. (2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时，l₁与l₂平行，即m=0或m=-1. (3)当-m(m-3)(m+1)=0且12-4m=0时，l₁与l₂重合，即m=3.

填空题

1、函数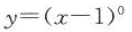的定义域为().

答 案：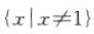

解 析：因为数学里规定：零的0次方没有意义。所以这里x-1≠0解得x≠1该函数的定义域为｛x|x≠1，x属于R｝

2、函数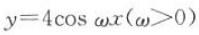的最小正周期为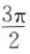,则=（）.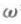

答 案：

解 析：根据题意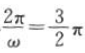得，解得