2024年成考高起点《数学(理)》每日一练试题12月01日
精选习题
2024-12-01
12:02:22
收藏
单选题
1、设f(x)=x3+ax2+x为奇函数,则a=()。
- A:1
- B:0
- C:
- D:-2 D.C.-1
答 案:B
解 析:本题主要考查的知识点为函数的奇偶性. 因为f(x)为奇函数,故f(-x)=-f(x)。即-x3+ax2-x=-x3-ax2-x,a=0。
2、下列各式中,不成立的是()。
- A:
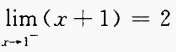
- B:
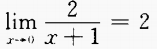
- C:
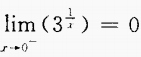
- D:
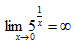
答 案:D
解 析:可用排除法,A、B、C均成立。
3、命题甲:实数a,b,c成等比数列;命题乙:b2=ac,则甲是乙()。
- A:充分条件但不是必要条件
- B:必要条件但不是充分条件
- C:充分必要条件
- D:不是充分条件也不是必要条件
答 案:A
4、一个袋子中装有标号分别为1,2,3,4的四个球,采用有放回的方式从袋中摸球两次,每次摸出一个球,则恰有一次摸出2号球的概率为()。
- A:
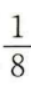
- B:

- C:
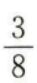
- D:

答 案:C
解 析:本题主要考查的知识点为独立重复试验的概率。 所求概率为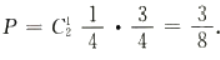
主观题
1、试证明下列各题
(1)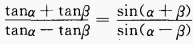
(2)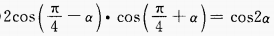
答 案:(1)化正切为正、余弦,通分即可得证。 (2)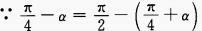

2、已知等差数列前n项和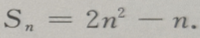 (Ⅰ)求这个数列的通项公式;(Ⅱ)求数列第六项到第十项的和
(Ⅰ)求这个数列的通项公式;(Ⅱ)求数列第六项到第十项的和
答 案: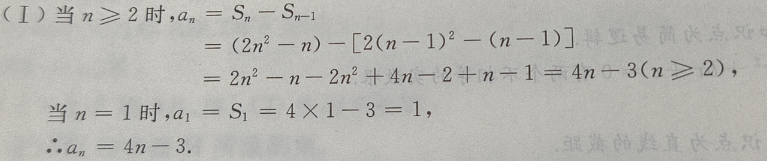

3、(1)已知tanα=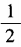 ,求cot2α的值; (2)已知tan2α=1,求tanα的值。
,求cot2α的值; (2)已知tan2α=1,求tanα的值。
答 案:(1)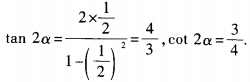 (2)由已知,得
(2)由已知,得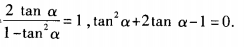 解关于tanα的一元二次方程,得tanα=
解关于tanα的一元二次方程,得tanα=
4、设a为实数,且tanα和tanβ是方程ax2+(2a-3)x+(a-2)=0的两个实根,求tan(α+β)的最小值。
答 案:由已知得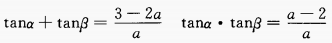

填空题
1、lgsinθ=a,lgcosθ=b,则sin2θ=______。
答 案:2×10a+b
解 析: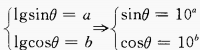 sin2θ=2sinθcosθ=2×10a×10b=2×10a+b
sin2θ=2sinθcosθ=2×10a×10b=2×10a+b
2、已知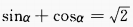 ,则
,则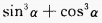 =______。
=______。
答 案:
解 析:

更多推荐

