判断题
1、函数y=1/x在(0,+∞)上单调递减。（）
答 案：对
2、满足不等式a≤x≤b的实数x的集合叫闭区间，表示为（a，b）。（）
答 案：错
单选题
1、若a>b，则下列不等式正确的是（）
- A：a的平方>b的平方
- B：2a＞2b
- C：3a＞2b
- D：｜a｜<｜b｜
答 案：B
2、下列关于圆的性质说法正确的是（）
- A：平分弦的直径垂直于弦
- B：三角形的内心是三条角平分线的交点
- C：在同圆或等圆中，相等的弦所对的圆周角相等
- D：三点确定一个圆
答 案：B
解 析：A、平分弦(不是直径)的直径垂直于弦，故选项错误，不符合题意；B、三角形的内心是三条角平分线的交点，故选项正确，符合题意；C、在同圆或等圆中，相等的弦所对的圆周角相等或互补，故选项错误，不符合题意；D、不在同一直线上的三点确定一个圆，故选项错误，不符合题意．故选：B
多选题
1、下列命题中，不正确的是（）
- A：三点可确定一个圆
- B：三角形的外心是三角形三边中线的交点
- C：一个三角形有且只有一个外接圆
- D：三角形的外心必在三角形的内部或外部
答 案：ABD
解 析：A、不在同一条直线上的三点确定一个圆，故本选项错误；B.、三角形的外心是三角形三边垂直平分线的交点，所以本选项是错误；C、三角形的外接圆是三条垂直平分线的交点，有且只有一个交点，所以任意三角形一定有一个外接圆，并且只有一个外接圆，所以本选项是正确的；D、直角三角形的外心在斜边中点处，故本选项错误。故选：ABD
2、设{an}(n∈N*)是各项为正数的等比数列，q是其公比，Kn是其前n项的积，且K5K8，则下列选项中成立的是()
- A：0
- B：a7＝1
- C：K9>K5
- D：K6与K7均为Kn的最大值
答 案：ABD
解 析：根据题意，依次分析选项：
对于B，若K6＝K7，则a7＝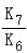
＝1，故B正确；
对于A，由K5＜K6可得a6＝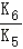
＞1，则q＝
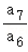∈（0，1），故A正确；
对于C，由{an}是各项为正数的等比数列且q∈（0，1）可得数列单调递减，则有K9＜K5，故C错误；
对于D，结合K5＜K6，K6＝K7＞K8，可得D正确．
故选：ABD．
主观题
1、已知两直线
,当m为何值时，l1与l2: (1)相交；(2)平行；(3)重合.
答 案：(1)当1×3m-(m-2)m2=-m2(m-2)+3m=-m(m-3)(m+1)≠0时，l1与l2相交，即m≠0,m≠3且m≠-1. (2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时，l1与l2平行，即m=0或m=-1. (3)当-m(m-3)(m+1)=0且12-4m=0时，l1与l2重合，即m=3.
2、已知函数f(x)=log3(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.
答 案：(1)根据题意可得，3x-1>0,解得
所以函数f(x)的定义域是
(2)因为f(x)=log3(3x-1)<1=log33,f(x)为定义域上的增函数，所以O<3x-1<3,解得
所以x的取值范围是
填空题
1、“|a|=1”是a=—1”的___________.
答 案：必要但不充分
2、以A(-1,1)，B(1,1)为直径端点的圆的方程是________.
答 案：x2+(y-1)2=1
