单选题

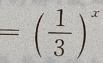1、函数与y的图像之间的关系是  

• A：关于原点对称
• B：关于x轴对称
• C：关于直线 y=1对称
• D：关于y轴对称

答 案：D

解 析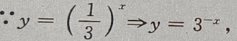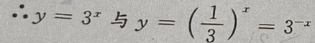：关于y轴对称，

2、已知sinx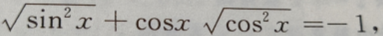，则x所在象限是（）  

• A：第一象限
• B：第二象限
• C：第三象限
• D：第四象限

答 案：C

解 析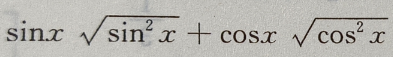：=sinx|sinx|+cosx|cosx|，当sinx、cosx均为负时，有 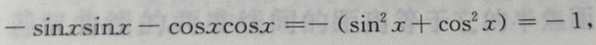故x在第三象限  

3、若A（-3，5），B（-5，-3），则线段AB中点的坐标为（）。  

• A：（4，-1）
• B：（-4，1）
• C：（-2，4）
• D：（-1，2）

答 案：B

4、已知点M(-2,5),N(4,2),点P在上，且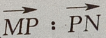=1:2，则点P的坐标为（）

• A：
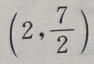
• B：(0,4)
• C：(8,2)
• D：(2,1)

答 案：B

解 析：由题意得：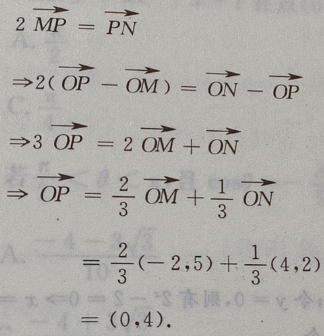  

主观题

1、求下列函数的最大值、最小值和最小正周期： （1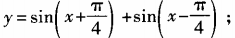） 2）y=6cosx+8sinx

答 案： 所以函数的最大值是最小值是最小正周期为2π， （2）要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式，需使cosx与sinx的系数平方和为1，为此，将已知函数化为 因此,函数的最大值是10,最小值是-10,最小正周期为2π

2、弹簧的身长与下面所挂砝码的重量成正比，知弹簧挂20g重的砝码时长度是12cm,挂35g重的砝码时长度是15cm，写出弹簧长度y(cm)与砝码重x(g)的函数关系式，并求弹簧不挂砝码时的长度

答 案：设弹簧原长为y0cm，则弹簧伸长量为（y-y0）cm， 由题意得y-y0=kx,即y=kx+y0, 由已知条件得 解得k=0.2，y0=8. 所求函数关系式为y=0.2x+8，弹的原长为8CM  

3、设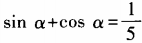（0＜α＜π），求tanα的值。  

答 案：

4、求函数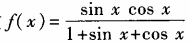（x∈R）的最大值与最小值。  

答 案：设sinx+cosx=t，则（sinx+cosx）²=t²，1+2sinxcosx=t²，sinxcosx= 于是转化为求的最值。 由所设知 上为增函数，故g（t）的最大值为最小值为

填空题

1、“x²=4”是“x=2”的______。  

答 案：必要不充分条件

2、与已知直线7x+24y-5=0平行，且距离等于3的直线方程是______。  

答 案：7x+24y+70=0或7x+24y-80=0

解 析：设要求的直线方程为7x+24y+c=0， ∵直线7x+24y+c=0到直线7x+24y-5=0的距离等于3 ∴ ∴.C=70或-80. 故所求的直线方程为7x+24y+70=0或7x+24y-80=0