单选题

1、曲线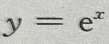与其过原点的切线及y轴所围面积为（）

• A：
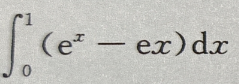
• B：
• C：
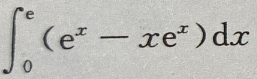
• D：

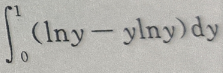
答 案：A

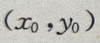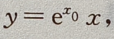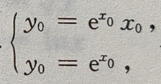解 析：设为切点，则切线方程为联立得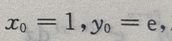所以切线方程为y=ex，故所求面积为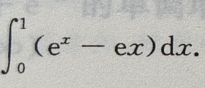

2、对于微分方程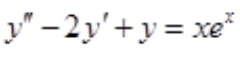，利用待定系数法求其特解y*时，下列特解设法正确的是（）。

• A：y*＝（Ax＋B）e^x
• B：y*＝x（Ax＋B）e^x
• C：y*＝Ax³e^x
• D：y*＝x²（Ax＋B）e^x

答 案：D

解 析：特征方程为r²－2r＋1＝0，特征根为r＝1（二重根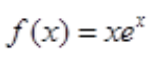），，a＝1为特征根，原方程特解为。

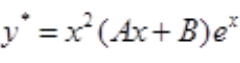3、下列不等式成立的是（）。  

• A：
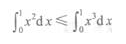
• B：
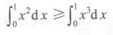
• C：
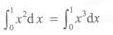
• D：

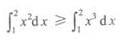
答 案：B

解 析：在[0，1]上，x²≥x³，由定积分的性质可知选B。同样在[1，2]上，x²≤x³，可知D不正确。

主观题

1、计算。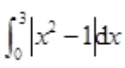

答 案：解：

2、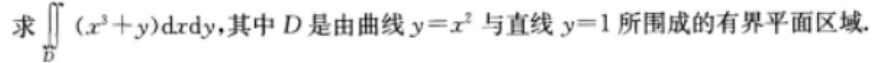

答 案：

3、将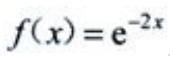展开为x的幂级数。

答 案：解：因为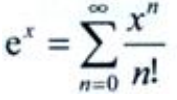，，所以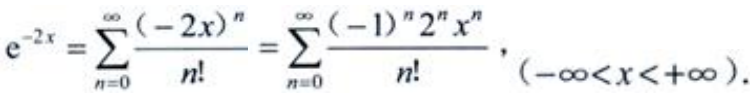

填空题

1、设函数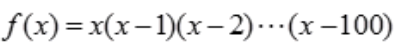，则f'(0)＝（）。

答 案：100！

解 析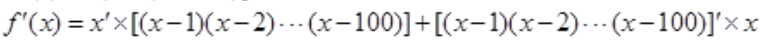：，则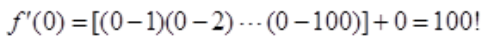

2、级数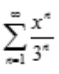的收敛区间是（）。

答 案：（-3,3）

解 析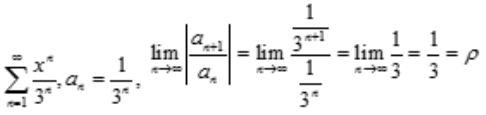：，因此收敛半径R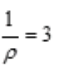＝，收敛区间为（－3,3）。

3、若级数条件收敛（其中k＞0为常数），则k的取值范围是（）。

答 案：0＜k≤l

解 析：k＞1时，级数各项取绝对值，得正项级数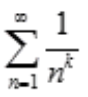，是收敛的p级数，从而原级数绝对收敛；当0＜k≤l时，由莱布尼茨交错级数收敛性条件可判明原级数条件收敛，因此应有0＜k≤1。

简答题

1、求微分方程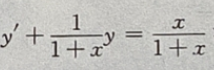满足初值条件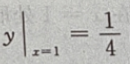的特解  

答 案：