单选题

1、设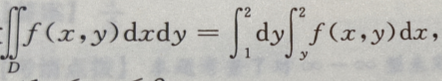则积分区域D可以表示为（）

• A：
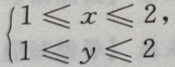
• B：
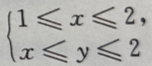
• C：
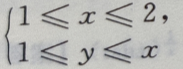
• D：

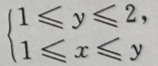
答 案：C

解 析：据右端的二次积分可得积分区域D为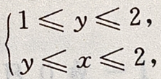选项中显然没有这个结果，于是须将该区域D用另一种不等式(X-型)表示，故D又可表示为

2、（）。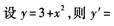  

• A：2x
• B：3+2x
• C：3
• D：x² 

答 案：A

解 析：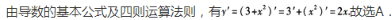

3、（）。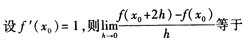  

• A：2
• B：1
• C：1/2
• D：0

答 案：A

解 析：

主观题

1、曲线y²＋2xy＋3＝0上哪点的切线与x轴正向所夹的角为？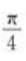

答 案：解：将y²＋2xy＋3＝0对x求导，得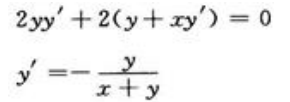欲使切线与x轴正向所夹的角为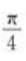，只要切线的斜率为1，即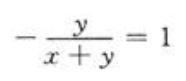亦即x＋2y＝0，设切点为（x₀，y₀），则x₀＋2y₀＝0①
又切点在曲线上，即y₀²＋2x₀y₀＋3＝0②
由①，②得y₀＝±1，x₀＝±2
即曲线上点（－2，1），（2，－1）的切线与x轴正向所夹的角为。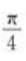

2、求。

答 案：解：。

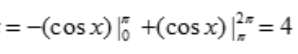3、求过两点M₁（1，－1，－2），M₂（－1，1，1）作平面，使其与y轴平行的平面方程。

答 案：解：所求平面法向量同时垂直y轴及向量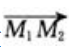，即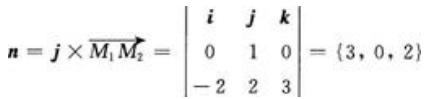由点法式可得所求平面为3x＋2z＋1＝0。

填空题

1、设函数f（x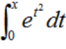）=，则f’（0）=______。  

答 案：1

解 析：由可变上限积分求导公式可知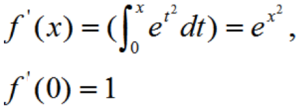

2、设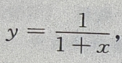则dy=（）  

答 案：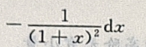

解 析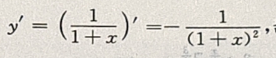：故有

3、＝（）。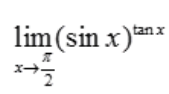

答 案：1

解 析：。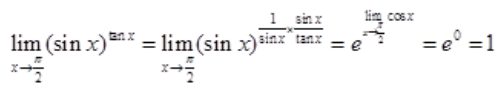

简答题

1、  

答 案：