单选题

1、若直线ax-y-2a-1=0与圆x²+y²-2x-1=0相切，则a的值是（）  

• A：2
• B：
• C：1
• D：

答 案：C

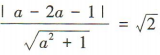解 析：由x²+y²-2x-1=0得(x-1)²+y²=2,则圆的圆心坐标为(1,0),半径为.由题意知圆心(1,0)到直线ax-y-2a-1=0的距离等于半径，即整理得(a-1)²=0,解得a=1.

2、已知数列{an}是等差数列，a3=2,公差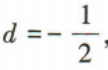则首项a1=（）

• A：3
• B：4
• C：5
• D：6

答 案：A

解 析：

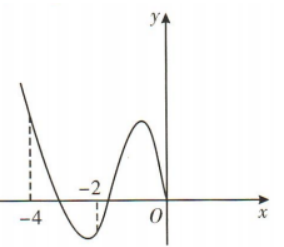
3、奇函数y=f(x)的部分图像如图所示，则（）

• A：
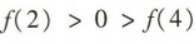
• B：
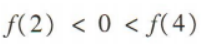
• C：
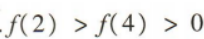
• D：

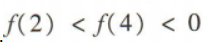
答 案：A

解 析：因为f(x)是奇函数，所以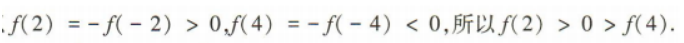

4、已知椭圆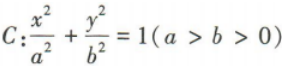的焦距为2√2,过原点O的直线交椭圆C于A,B两点，P是椭圆C上另外一点，若直线PA,PB的斜率之积为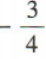,则椭圆C的方程为()

• A：
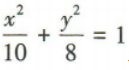
• B：
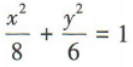
• C：
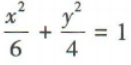
• D：

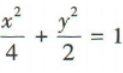
答 案：B

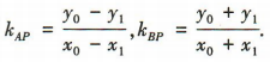
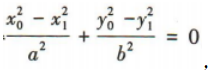
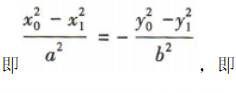
解 析：由题意设P(x_0,y₀),A(x₁,y₁),B(-x₁,-y₁),则 所以，又c=√2,c²=a²-b²,所以a²=8,b²=6,所以椭圆C的方程为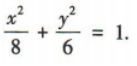

填空题

1、已知椭圆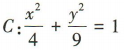与直线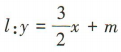交于A,B两点,则实数m的取值范围为()  

答 案：

解 析：由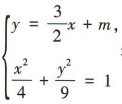得9x²+6mx+2m²-18=0.因为直线l与椭圆C交于A,B两点,所以Δ=36m²-36(2m²-18)= 36(18-m²)>0,解得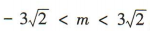,故实数m的取值范围为.

2、若(x-1)ⁿ的展开式中x²的系数是-10,则n的值为()  

答 案：5

解 析：因为(x-1)ⁿ的展开式中x²的系数是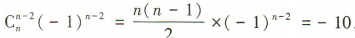,所以n= 5.

3、各棱长都为1的正三棱锥的体积是（）  

答 案：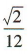

解 析：易知该正三棱锥的底面积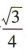为，高为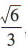，故该正三校锥的体积为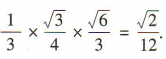

4、已知集合A={1.2.3},B={a,3.4}.若A∩B={2,3},则a=（）  

答 案：2

解 析：∵A∩B={2,3},所以2∈B,又B={a,3,4},∴a=2.

简答题

1、已知平面直角坐标系中，A(1,0),B(0,1),C(2,5). (1)求向量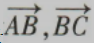的坐标； (2)若四边形ABCD为平行四边形，求点D的坐标.

答 案：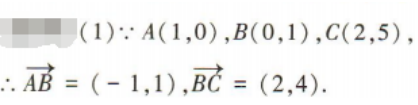

2、已知2＜a＜3,-2＜b＜3. (1)求3a+b的取值范围； (2)求a-b的取值范围.

答 案：(1)∵2＜a＜3, ∴6＜3a＜9, 又-2＜b＜3,∴4＜3a+b＜12. (2)∵-2＜b＜3,∴-3＜-b＜2, 又∵2＜a＜3,∴-1＜a-b＜5.