单选题

1、函数y=sin（x+11）的最大值是（）。

• A：11
• B：1
• C：-1
• D：-11

答 案：B

解 析：本题主要考查的知识点为三角函数的值域。 因为-1≤sin（wx+q）≤1，所以-1≤sin（x+11）≤1，故y=sin（x+11）的最大值为1。

2、已知sinα=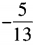，且540°＜α＜630°，则sin2α=（）。

• A：
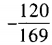
• B：
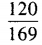
• C：
• D：

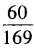
答 案：B

解 析：由已知，360°+180°＜α＜360°+270°，所以α是第三象限的角，故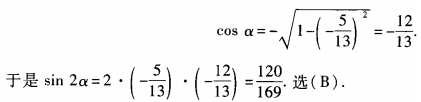

3、若a，b，c分别表示△ABC的顶点A，B，C所对的边长，且（a+b+c）（a+b-c）=3ab，cos（A+B）=（）。

• A：
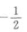
• B：
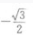
• C：
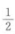
• D：

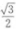
答 案：A

4、已知一个等差数列的第五项等于10，前三项的和等于3，那么这个等差数列的公差为（）。

• A：3
• B：1
• C：-1
• D：-3

答 案：A

主观题

1、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.
(I）求l与C的准线的交点坐标；
(II）求|AB|．

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由得设A（x1,y1）.B（x2,y2），则因此

2、设3^a=5^b=15，求a^-1+b^-1的值。  

答 案：由3^a=15，得a=log₃15；又由5^b=15，得b=log₅15。 因此a^-1+b^-1=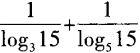 =log₁₅3+log₁₅5=1。

解 析：过程中应用了换底公式的推论，即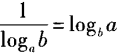

3、计算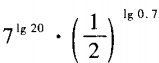  

答 案：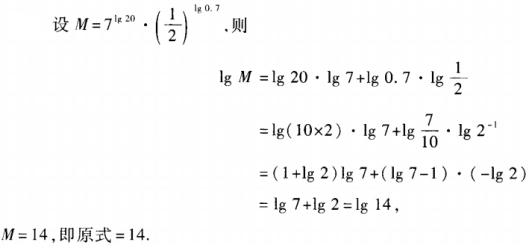

4、求下列函数的最大值、最小值和最小正周期： （1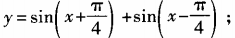） 2）y=6cosx+8sinx

答 案： 所以函数的最大值是最小值是最小正周期为2π， （2）要将6cosx+8sinx化为sinαcosx+cosαsinx这种形式，需使cosx与sinx的系数平方和为1，为此，将已知函数化为 因此,函数的最大值是10,最小值是-10,最小正周期为2π

填空题

1、“a＞b”是“a-c＞b-c”的______。

答 案：充要条件

2、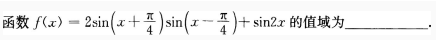  

答 案：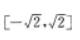

解 析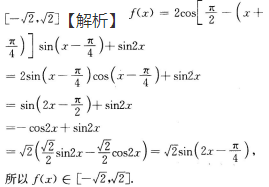： 【考点指要】本题主要考查三角函数的最大值、最小值及值域的求法，解题时需要灵活运用诱导公式、二倍角公式以及辅助角公式，当函数可以化