单选题
1、一道数学试题,甲、乙两位同学独立完成,设命题p是“甲同学解出试题”,命题q是“乙同学解出试题”,则命题“至少一位同学解出试题”可表示为()
答 案:D
解 析:“至少一位同学解出试题”即“甲同学解出试题或乙同学解出试题”,所以命题“至少一位同学解出试题”可表示为p∨q.
2、不等式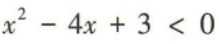 的解集为()
的解集为()
答 案:C
解 析: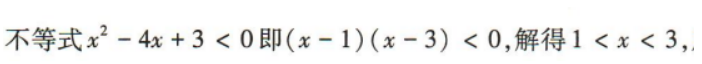

3、甲、乙、丙、丁4名同学站成一排拍照,若甲不站在两端,则不同的排列方式有
答 案:B
解 析:甲不同站位的排列数为 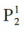 ,其余三位学生不同站位的全排列数为
,其余三位学生不同站位的全排列数为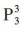 ,所以所有的排列方式有
,所以所有的排列方式有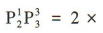

4、有4名学生报名参加数学、物理、化学竟赛,每人限报一科,则不同的报名方法有()
答 案:A
解 析:根据题意可知,每名同学都有数学、物理、化学三种科目可报,所以不同的报名方法种数为3x3x3x3 = 81.
填空题
1、若复数(m2-2m)+ mi 是纯虚数,则实数 m 的值为()
答 案:2
解 析:因为复数(m2-2m)+ mi 是纯虚数,所以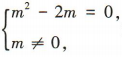 解得 m = 2.
解得 m = 2.
2、如图,画一个边长为4的正方形,再将这个正方形各边的中点相连得到第2个正方形,依此类推,这样一共画了10个正方形,则第10个正方形的面积为()

答 案: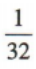
解 析:由题意知,第一个正方形的边长a1=4,面积T1=16;第二个正方形的边长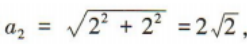 面积T2=8;第三个正方形的边长a3=2,面积T3=4;第四个正方形的边长
面积T2=8;第三个正方形的边长a3=2,面积T3=4;第四个正方形的边长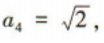 面积T4=2,……,由此可发现规律,第n个正方形的面积
面积T4=2,……,由此可发现规律,第n个正方形的面积
3、如图,在长方体ABCD-A1B1C1D1中,AB=1,AD=2,AA1=2,则二面角A-DD1-B的正切值为()

答 案: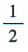
解 析:易得 ,
, 平面角.在
平面角.在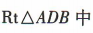 ,AB=1AD=2,
,AB=1AD=2,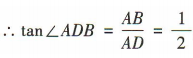 ,∴二面角A-DD1-B的正切值为
,∴二面角A-DD1-B的正切值为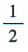 .
.
4、若角α的顶点与坐标原点重合,始边与x轴非负半轴重合,终边经过点(1,1),则sinα=()
答 案: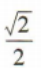
解 析:
简答题
1、已知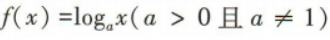 的图像过点(4,2).
(1)求a的值;
(2)当
的图像过点(4,2).
(1)求a的值;
(2)当 时,求f(x)的取值范围;
(3)若g(x)=f(1-x)-f(1+x),判断g(x)的奇偶性.
时,求f(x)的取值范围;
(3)若g(x)=f(1-x)-f(1+x),判断g(x)的奇偶性.
答 案:
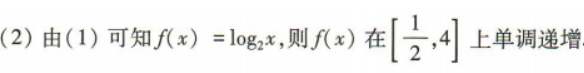
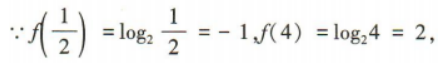

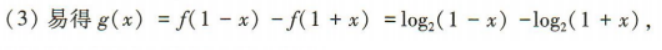

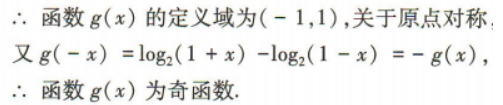
2、从6名男生和4名女生中随机选出3名同学参加一项竞技测试.
(1)求选出的3名同学中至少有1名女生的概率;
(2)设ξ表示选出的3名同学中男生的人数,求ξ的分布列.
答 案:(1)由题意可知,选出的3名同学全是男生的概率为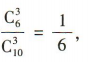 所以选出的3名同学中至少有1名女生的概率为
所以选出的3名同学中至少有1名女生的概率为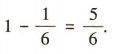 (2)根据题意,ξ的可能取值为 0,1,2,3,
则
(2)根据题意,ξ的可能取值为 0,1,2,3,
则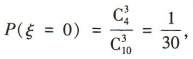
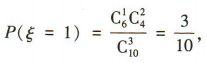

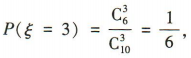 所以ξ的分布列为
所以ξ的分布列为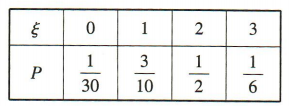

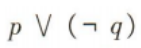


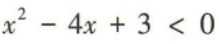 的解集为()
的解集为()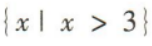
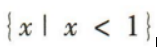
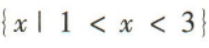
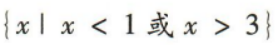
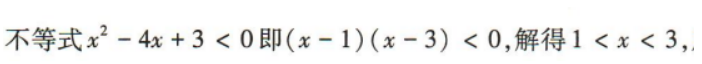

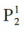 ,其余三位学生不同站位的全排列数为
,其余三位学生不同站位的全排列数为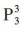 ,所以所有的排列方式有
,所以所有的排列方式有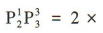

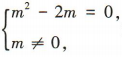 解得 m = 2.
解得 m = 2.
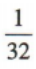
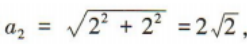 面积T2=8;第三个正方形的边长a3=2,面积T3=4;第四个正方形的边长
面积T2=8;第三个正方形的边长a3=2,面积T3=4;第四个正方形的边长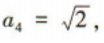 面积T4=2,……,由此可发现规律,第n个正方形的面积
面积T4=2,……,由此可发现规律,第n个正方形的面积

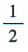
 ,
, 平面角.在
平面角.在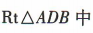 ,AB=1AD=2,
,AB=1AD=2,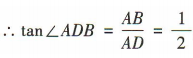 ,∴二面角A-DD1-B的正切值为
,∴二面角A-DD1-B的正切值为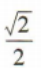

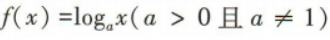 的图像过点(4,2).
(1)求a的值;
(2)当
的图像过点(4,2).
(1)求a的值;
(2)当 时,求f(x)的取值范围;
(3)若g(x)=f(1-x)-f(1+x),判断g(x)的奇偶性.
时,求f(x)的取值范围;
(3)若g(x)=f(1-x)-f(1+x),判断g(x)的奇偶性.
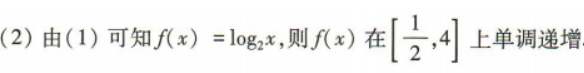
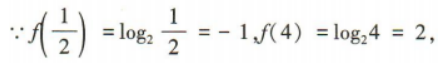

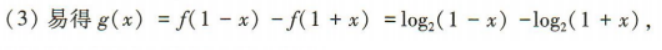

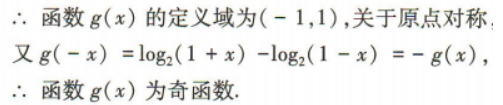
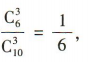 所以选出的3名同学中至少有1名女生的概率为
所以选出的3名同学中至少有1名女生的概率为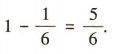 (2)根据题意,ξ的可能取值为 0,1,2,3,
则
(2)根据题意,ξ的可能取值为 0,1,2,3,
则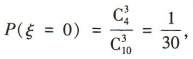
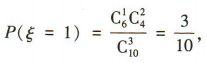

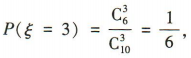 所以ξ的分布列为
所以ξ的分布列为

