单选题

1、在正方体 ABCD-A₁B₁C₁D₁的棱所在的直线中,与直线 AC 异面的直线有()  

• A：3条
• B：4 条
• C：6条
• D：8条

答 案：C

解 析：易知在正方体 ABCD-A₁B₁C₁D₁的棱所在的直线中与直线 AC 异面的直线有 BB₁,DD₁,A₁D₁,B₁A₁,B₁C₁,C₁D₁,共6条.

2、已知A(0,2),B(4,-8),则线段AB的中点坐标为()  

• A：(-2,-3)
• B：(2,3)
• C：(-2,3)
• D：(2,-3)

答 案：D

解 析：因为A(0,2),B(4,-8),所以线段AB的中点坐标为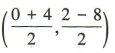,即(2,-3).

3、若椭圆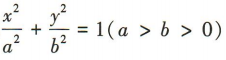的焦距为2,离心率为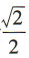,则椭圆的方程为()  

• A：
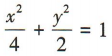
• B：
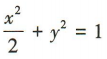
• C：
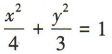
• D：

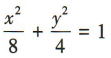
答 案：B

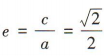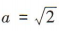解 析：由题意可知 2c = 2,即c=1.由椭圆的离心率得,所以b²=α²-c²=1,所以椭圆的标准方程为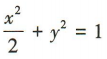

4、函数f(x)=x²-2x的单调递增区间为

• A：(-∞,1]
• B：[1,+∞)
• C：(-∞,-1]
• D：[1,+∞)

答 案：B

解 析：易知函数f(x)=x²-2x=(x-1)²-1的图像开口向上，其对称轴为直线x=1,所以f(x)的单调递增区间为[1,+∞)    

填空题

1、已知函数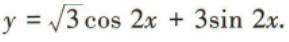 求： (1)函数的值域； (2)函数的最小正周期； (3)函数取得最大值时x的取值集合.

答 案：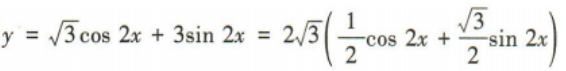

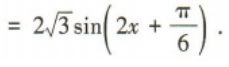
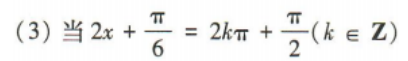
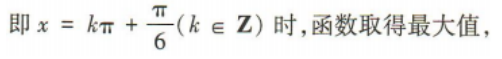
2、已知|a|=2,|b|=4,a·b=-4,则向量a与b的夹角为（）  

答 案：5

解 析：

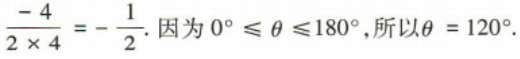
3、若事件A为必然事件,则其对立事件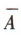的概率等于（）  

答 案：0

解 析：因为事件A为必然事件,所以事件A的概率 P(A)=1,所以对立事件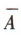的概率为 0.

4、袋中装有大小、形状完全相同的6个白球,4个红球,从中任取一球,则取到白球的概率为（）  

答 案：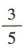

解 析：因为一共有 10 个球,所以从中任取一球的基本事件有 10个,又有6个白球,所以取到白球的基本事件有6个,所以取到白球的概率为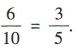

简答题

1、如图,已知四棱锥P-ABCD的底面ABCD是矩形,,AB=PD=4,AD=2,点E,F分别是 AB,PC的中点. 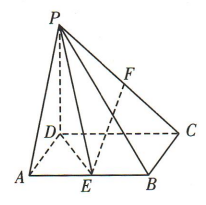(1)证明:EF//平面PAD.
(2)求三棱锥E-PAD 的体积.  

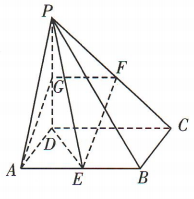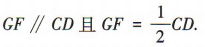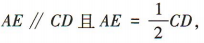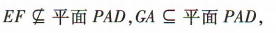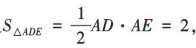答 案：(1)取 PD 中点 G,连接 GF,AG. 因为G,F分别是PD,PC的中点， 所以 又因为底面 ABCD 为矩形,E为AB 中点, 所以 所以GF//AE 且GF = AE, 所以四边形 CFEA 为平行四边形, 所以 GA // EF. 又 所以EF//平面PAD. (2)因为 所以 PD 为三棱锥P-AED 的高. 又 所以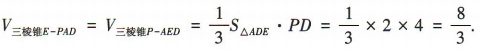  

2、某地有一座水库，最大容量为128000m³.根据预测，汛期时水库的进水量S(单位：m³)与天数n(n∈N*)的关系是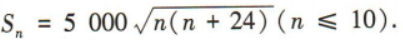水库原有水量为80000m³,每天泄水量为4000m³.当汛期来临第一天，水库就开始泄洪，估计汛期将持续10天，问此期间堤坝会发生危险吗?请说明理由(水库水量超过最大容量，堤坝就会发生危险).

答 案：设第n天发生危险.由题意得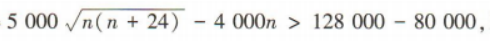 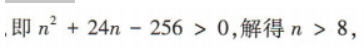所以汛期的第9天会有危险.