2024年成考专升本《高等数学一》每日一练试题11月01日
精选习题
2024-11-01
11:40:20
收藏
单选题
1、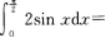
（）
- A：1/2
- B：1
- C：2
- D：3
答 案：C
2、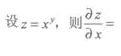
（）。
- A：
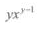
- B：
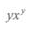
- C：
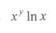
- D：
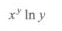
答 案：A
解 析：
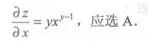
3、
（）。
- A：
- B：
- C：
- D：
答 案：D
解 析：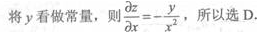
主观题
1、计算
答 案：解：令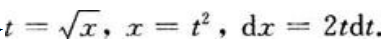
当x＝4时，t＝2；当x＝9时，t＝3。则有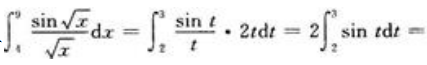
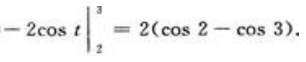
2、将函数
展开成x的幂级数，并指出其收敛区间
答 案：解：因为
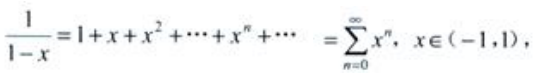所以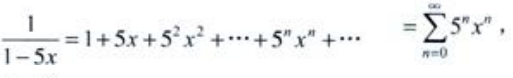
其中5x∈（-1，1），得收敛区间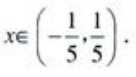
3、求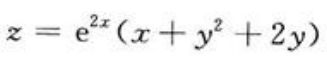
的极值．
答 案：解：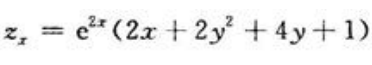
，
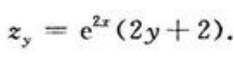故由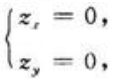
得驻点（1/2，－1），
于是
，且
。故（1/2，－1）为极小值点，且极小值为
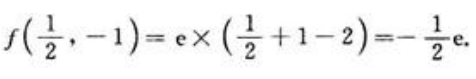
填空题
1、已知函数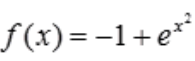
在[－1，1]上满足罗尔定理的条件，那么由定理所确定的
＝（）。
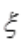答 案：
解 析：
，解得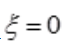
。
2、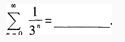
答 案：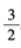
解 析：由等比级数和的公式有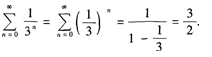
3、
（）。
答 案：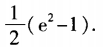
解 析：本题考查的知识点为定积分计算。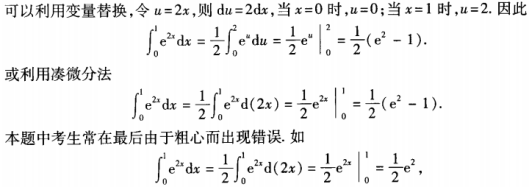
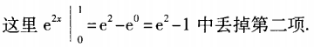
简答题
1、
（1）将f（x）展开为x的幂级数；
（2）利用（1）的结果，求数项级数
的和。
答 案：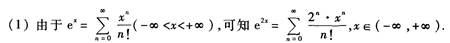
（2）在上述展开式中，令x=1，可得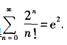
更多推荐
