判断题

1、已知集合A={x|x²-3x-4=0}，B={0，1，4，5}，则A∩B中元素的个数为0。（）  

答 案：错

解 析：由A中方程变形得：（x-4）（x+1）=0，
解得：x=4或x=-1，即A={-1，4}，
∵B={0，1，4，5}，
∴A∩B={4}，交集中元素的个数为1个．

2、圆（x-2）²+（y+1）²=4的半径为2。（）  

答 案：对

单选题

1、设a=log₃2，b=log₂3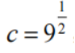，，则a，b，c的大小关系是（）  

• A：a＞c＞b
• B：c＞b＞a
• C：b＞c＞a
• D：c＞a＞b

答 案：B

解 析：log₃3=1，log₃2＜log₃3所以a＜1。log₂2=1,log₂4=2,log₂2＜log₂3＜log₂4,所以1＜b＜2，c=3，综上选B

2、已知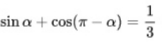，则sin2a的值为（）  

• A：8/9
• B：1/9
• C：-8/9
• D：4/9

答 案：A

多选题

1、已知等差数列{a_n}的前n项和为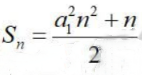，公差为d，则（）  

• A：a₁=1
• B：d=1
• C：2S_n-a_n=1+3+5+...+(2n-1)
• D：

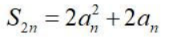
答 案：ABC

2、已知向量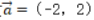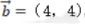，，则（）  

• A：
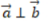
• B：
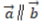
• C：
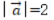
• D：

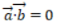
答 案：AD

解 析：若设a=(x1,y1)，b=(x2,y2)，a⊥b的充要条件是a·b=0，即(x1x2+y1y2)=0。本题中-2*4+2*4=0，则两个向量垂直

主观题

1、已知等差数列{an}的前n项和S_n且S₅=35,S₈=104.
(1)求数列{an}的通项公式；
(2)若{b_n}为等比数列，b₁=a₂,b₂=a₃+2,求数列{b,}的公比q及前n项和T_n.

答 案：(1)所以a₆=19.则数列{an}的公差，通项公式为an=a₆+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以则

2、已知两直线,当m为何值时，l₁与l₂: (1)相交；(2)平行；(3)重合.  

答 案：(1)当1×3m-(m-2)m²=-m²(m-2)+3m=-m(m-3)(m+1)≠0时，l₁与l₂相交，即m≠0,m≠3且m≠-1. (2)当-m(m-3)(m+1)=0且1×2m-(m-2)×6=12-4m≠0时，l₁与l₂平行，即m=0或m=-1. (3)当-m(m-3)(m+1)=0且12-4m=0时，l₁与l₂重合，即m=3.

填空题

1、把多项式x⁴y+2x²y³-5xy⁴+6-3x³y²按x的升幂排列是_____  

答 案：6-5xy⁴+2x²y³-3x³y²+x⁴y

解 析：是升幂，不是降幂

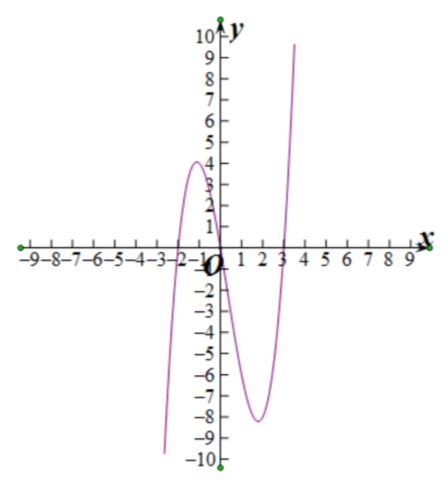
2、不等式x(x-3)(x+2)<0的解集为_____.  

答 案：（-∞，-2）∪（0，3）

解 析：作出函数f(x)=x(x-3)(x+2)的图像，由图像可得，不等式x(x-3)(x+2) < 0的解集是{ x|x＜-2或0综上所述，结论是:不等式x(x一3)(x+2) <0的解集是{ x|x＜-2或0