2024年成考专升本《高等数学二》每日一练试题10月27日
精选习题
2024-10-27
11:43:29
收藏
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、设函数y=x2+1,则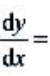 ().
().
- A:
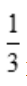 x3
x3 - B:x2
- C:2x
- D:
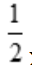 x
x
答 案:C
解 析: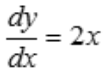 .
.
2、有两箱同种零件,第一箱内装50件,其中一等品10件;第二箱内装30件,其中一等品18件;现随机地从两箱中挑出一箱,再从这箱中随机地取出一件零件,则取出的零件是一等品的概率为()
- A:
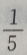
- B:
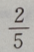
- C:
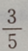
- D:
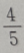
答 案:B
解 析:设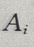 ={挑出的是第i箱},i=1,2;B={取出的是一等品},由题意知,
={挑出的是第i箱},i=1,2;B={取出的是一等品},由题意知,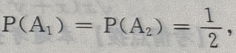
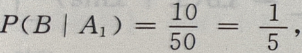
 由全概率公式知:
由全概率公式知: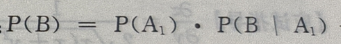 +
+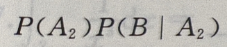
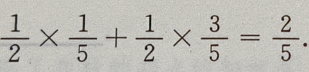
主观题
1、设函数y=y(x)是由方程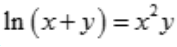 所确定的隐函数,求函数曲线y=y(x)过点(0,1)的切线方程.
所确定的隐函数,求函数曲线y=y(x)过点(0,1)的切线方程.
答 案:解:方程 两边对x求导数
两边对x求导数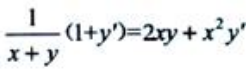 解得
解得 则
则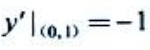 .切线方程为y-1=(-1)x,即x+y-1=0.
.切线方程为y-1=(-1)x,即x+y-1=0.
2、一枚2分硬币,连续抛掷3次,设A={至少有一次国徽向上}.求P(A).
答 案:解:一枚2分硬币连续抛掷3次出现的基本事件共有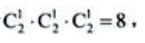 则
则 ={全部是字面向上},
={全部是字面向上},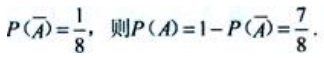
填空题
1、若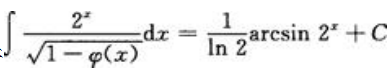 ,则
,则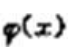 =().
=().
答 案:4x
解 析: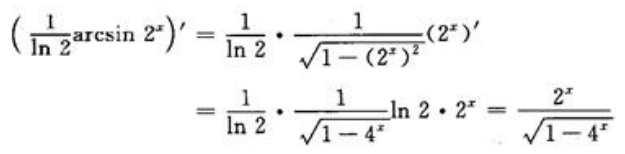 根据不定积分定义可知,有
根据不定积分定义可知,有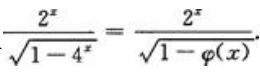 故
故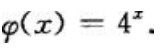
2、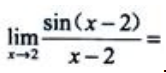 ().
().
答 案:1
解 析:由等价无穷小可知,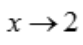 时,即
时,即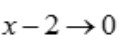 ,
,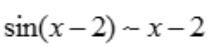 ,故
,故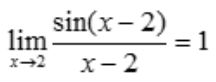 .
.
简答题
1、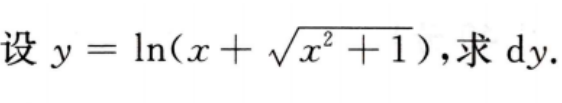
答 案: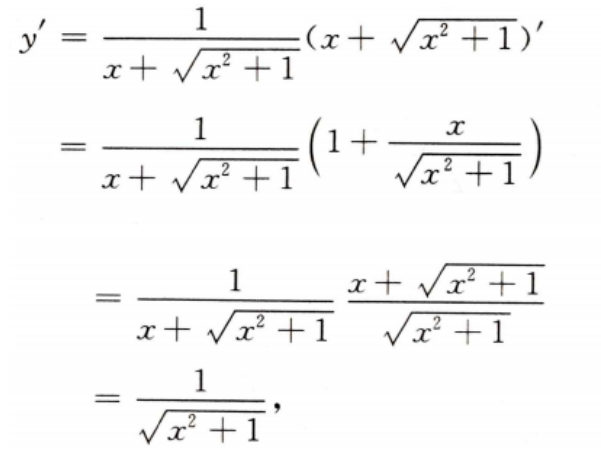

2、设事件A与B相互独立,且P(A)=0.6,P(B)=0.7,求P(A+B)。
答 案:本题考查事件相互独立的概念及加法公式。 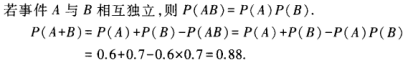
更多推荐

