2024年成考专升本《高等数学二》每日一练试题10月25日
精选习题
2024-10-25
11:28:59
收藏
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、设函数f(x)=x3+e3+3x,则f’(x)等于()。
- A:
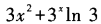
- B:
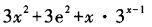
- C:
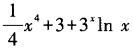
- D:
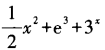
答 案:A
解 析:本题考查的知识点是基本初等函数的导数公式。只需注意e3是常数即可。
2、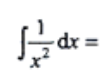 ().
().
- A:
 +C
+C - B:lnx2+C
- C:
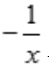 +C
+C - D:
 +C
+C
答 案:C
解 析:根据积分公式可得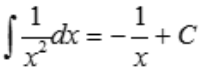 .
.
主观题
1、计算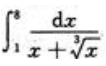 .
.
答 案:解:设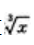 =t,得x=t3,所以dx=3t2dt当x=1时,t=1;当x=8时,t=2.所以
=t,得x=t3,所以dx=3t2dt当x=1时,t=1;当x=8时,t=2.所以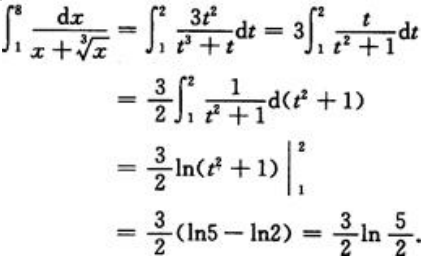
2、在抛物线y=1-x2与x轴所组成的平面区域内,做一内接矩形ABCD,其一条边AB在x轴上(如图所示)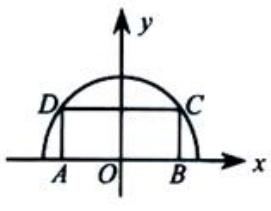 .设AB长为2x,矩形面积为S(x). (1)写出S(x)的表达式;
.设AB长为2x,矩形面积为S(x). (1)写出S(x)的表达式;
(2)求S(x)的最大值.
答 案:解:(1)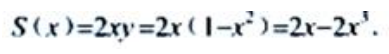
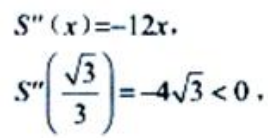 (2)
(2)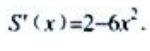 令
令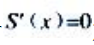 解得
解得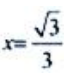 (
(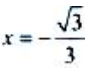 舍去)。则
舍去)。则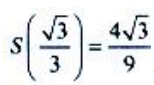 为极大值.由于驻点唯一,且实际问题有最大值,所以
为极大值.由于驻点唯一,且实际问题有最大值,所以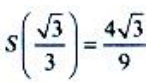 为最大值.
为最大值.
填空题
1、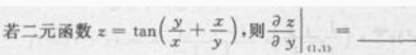 。
。
答 案:0
解 析: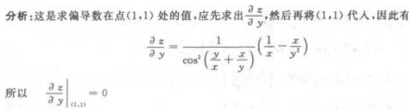
2、函数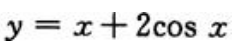 在
在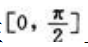 上最大值为().
上最大值为().
答 案: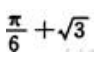
解 析:由 得驻点为
得驻点为 ,
, ,比较得y的最大值为
,比较得y的最大值为
简答题
1、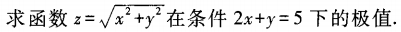
答 案:本题考查的知识点是条件极值的计算。 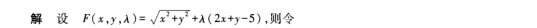

解 析:
2、甲、乙二人单独译出某密码的概率分别为0.6和0.8,求此密码被破译的概率。
答 案:本题考查的知识点是事件相互独立的概念和概率的加法公式。 
更多推荐

