判断题

1、若，则。（）  

答 案：错

解 析：所以  

单选题

1、（）。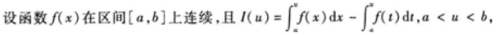  

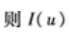• A：恒大于零
• B：恒小于零
• C：恒等于零
• D：可正、可负

答 案：C

解 析：定积分的值仅仅与被积函数和积分的上、下限有关，而与积分变量用什么字母表示无关。

2、若函数f（x）的导数f'（x）=-x＋1，则（）

• A：f（x）在（一∞，＋∞）单调递减
• B：f（x）在（一∞，＋∞）单调递增
• C：f（x）在（一∞，1）单调递增
• D：f（x）在（1，＋∞）单调递增

答 案：C

解 析：当x<1时，f'（x）=-x+1>0，故函数的单调递增区间为（-∞，1）；当x>1时，f'（x）=-x+1 <0，故函数的单调递减区间为（1，＋∞）.因此选C选项.

主观题

1、设平面图形是由曲线y＝和x＋y＝4围成的．（1）求此平面图形的面积S．
（2）求此平面图形绕x轴旋转而成的旋转体的体积V_x．

答 案：解：曲线y＝和x＋y＝4围成的图形如图阴影部分所示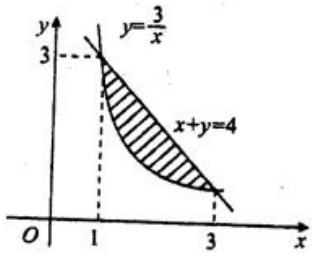．求两条曲线的交点，解方程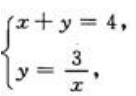得交点（1，3）与（3，1）．（1）面积；
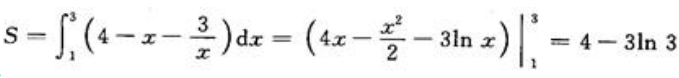（2）旋转体体积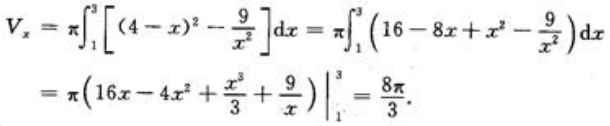

2、求函数f（x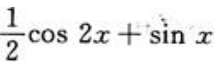）＝，在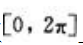上的最大值和最小值．

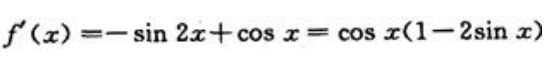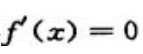答 案：解：，令，在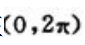内解得驻点为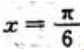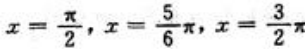，，求出以上各点及端点处函数值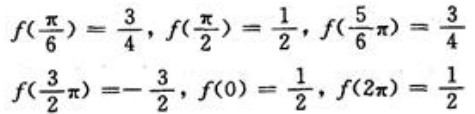比较可得，f（x）在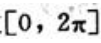上最大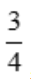值为，最小值为．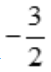

填空题

1、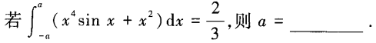  

答 案：1

解 析：被积函数的前一部分是奇函数，后一部分是偶函数，因此有： 解得a=1。  

2、已知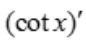＝f(x)，则()．

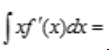答 案：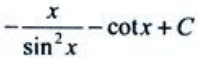

解 析：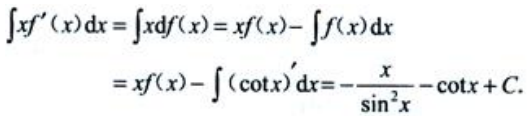

简答题

1、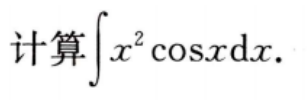  

答 案：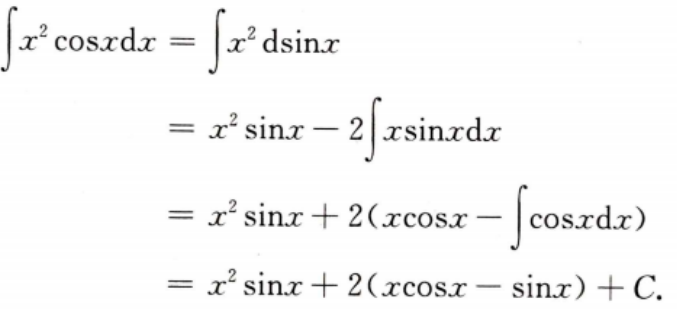

2、试确定a，b的值，使函数f(x)=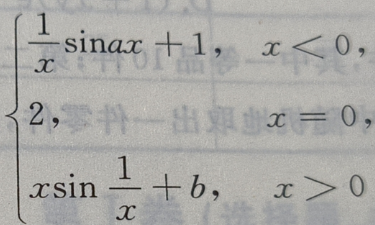在点x=0处连续。

答 案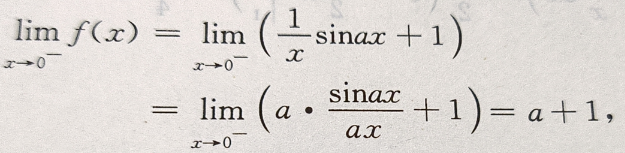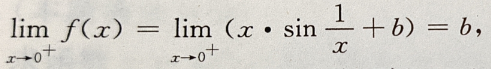： 因为f(x)在x=0处连续，则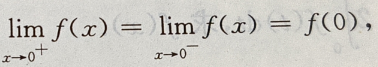即a+1=b=2，即a=1，b=2.