2024年成考专升本《高等数学二》每日一练试题10月21日
精选习题
2024-10-21
11:36:43
收藏
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、设函数z=xey,则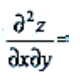 ().
().
- A:ex
- B:ey
- C:xey
- D:yex
答 案:B
解 析: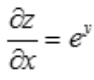 ,
,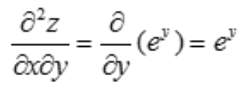 .
.
2、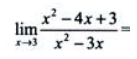 ( ).
( ).
- A:0
- B:1
- C:
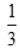
- D:
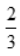
答 案:D
解 析: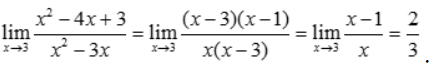
主观题
1、求二元函数f(x,y)=x2+y2+2y的极值.
答 案:解: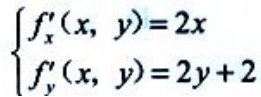 ,令
,令 ,得驻点(0,-1).因为
,得驻点(0,-1).因为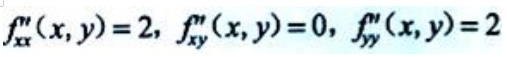
所以
由于A>0且 ,故f(x,y)在点(0,1)处取得极小值,极小值为f(0,-1)=-1.
,故f(x,y)在点(0,1)处取得极小值,极小值为f(0,-1)=-1.
2、求函数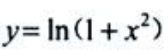 的单调区间、极值、凹凸区间和拐点.
的单调区间、极值、凹凸区间和拐点.
答 案:解:函数定义域为x∈R,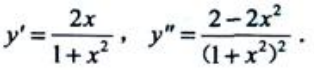 令y'=0得x=0,令y"=0得x=±1.函数
令y'=0得x=0,令y"=0得x=±1.函数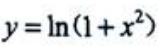 的单调增加区间为(0,+∞),单调减少区间为(∞,0);y(0)=0为极小值,无极大值.
的单调增加区间为(0,+∞),单调减少区间为(∞,0);y(0)=0为极小值,无极大值.
函数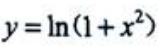 的凸区间为(-∞,-1)∪(1,+∞),凹区间为(-1,1),拐点为(-1,ln2)与(1,ln2).
的凸区间为(-∞,-1)∪(1,+∞),凹区间为(-1,1),拐点为(-1,ln2)与(1,ln2).
填空题
1、 =()
=()
答 案:
解 析:
2、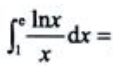 ()
()
答 案: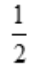
解 析: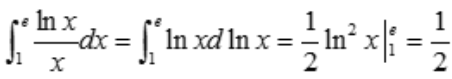 .
.
简答题
1、求函数ƒ(x,y)=x2+y2在条件2x+3y=1下的极值
答 案:解设F(x,y,λ)=x2+y2+λ(2x+3y-1), 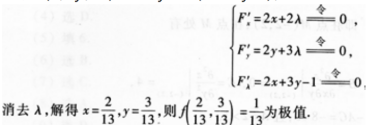
2、设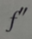 存在,
存在,
答 案: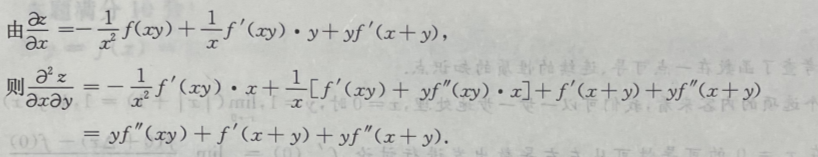
更多推荐

