判断题

1、若，则。（）  

答 案：错

解 析：所以  

单选题

1、有两箱同种零件,第一箱内装50件,其中一等品10件;第二箱内装30件,其中一等品18件;现随机地从两箱中挑出一箱,再从这箱中随机地取出一件零件，则取出的零件是一等品的概率为（）  

• A：
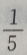
• B：
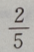
• C：
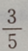
• D：

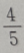
答 案：B

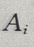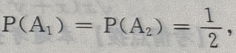
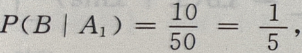
解 析：设={挑出的是第i箱}，i=1,2；B={取出的是一等品}，由题意知，由全概率公式知：+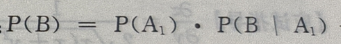

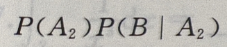
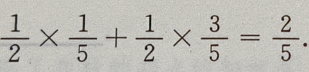
2、不定积分等于（）

• A：
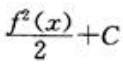
• B：
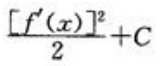
• C：
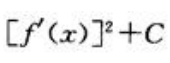
• D：

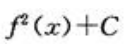
答 案：A

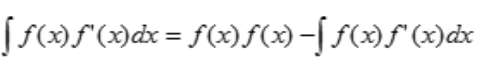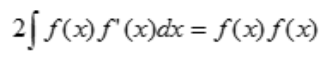解 析：由分部积分法可知，所以有即.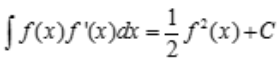

主观题

1、设函数y=y(x)是由方程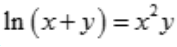所确定的隐函数，求函数曲线y=y(x)过点（0，1）的切线方程．

答 案：解：方程两边对x求导数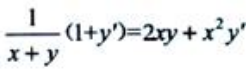解得则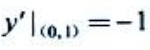．切线方程为y－1＝（－1）x，即x＋y－1＝0．

2、求．

答 案：解：

填空题

1、已知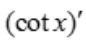＝f(x)，则()．

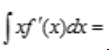答 案：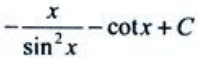

解 析：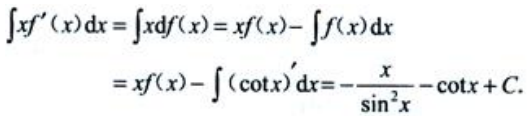

2、（）．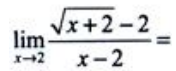

答 案：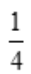

解 析：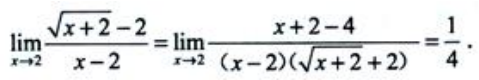

简答题

1、求函数的单调区间、极值及函数曲线的凸凹性区间、拐点和渐近线.

答 案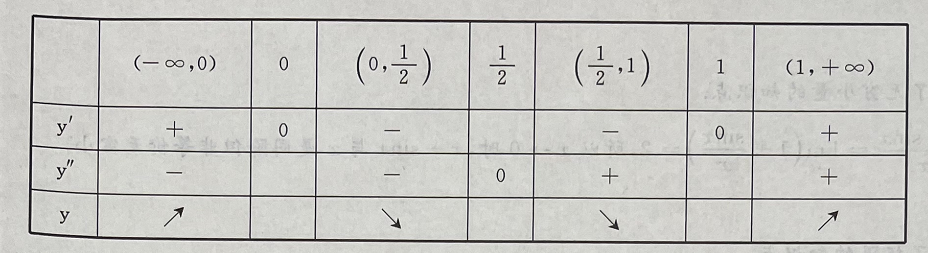：所以函数y的单调增区间为单调减区间为（0,1）；函数y的凸区间为凹区间为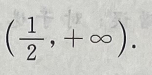故x=0时，函数有极大值0，x=1时，函数有极小值-1，且点为拐点，因不存在，且没有无意义的点，故函数没有渐近线。

2、求函数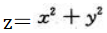在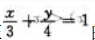条件下的极值及极值点．  

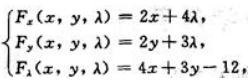答 案：令于是 求解方程组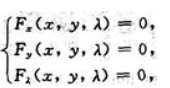得其驻点故点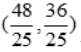为极值点，且极值为