2024年成考专升本《高等数学二》每日一练试题10月16日
精选习题
2024-10-16
11:39:13
收藏
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、设函数y=cosx+1,则dy=().
- A:(sinx+1)dx
- B:(cosx+1)dx
- C:-sinxdx
- D:sinxdx
答 案:C
解 析: ,故
,故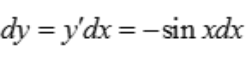 .
.
2、设函数f(x)=x3+e3+3x,则f’(x)等于()。
- A:
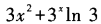
- B:
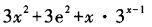
- C:
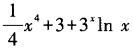
- D:
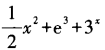
答 案:A
解 析:本题考查的知识点是基本初等函数的导数公式。只需注意e3是常数即可。
主观题
1、甲袋中有15只乒乓球,其中3只白球,7只红球,5只黄球,乙袋中有20只乒乓球,其中10只白球,6只红球,4只黄球.现从两袋中各取一只球,求两球颜色相同的概率.
答 案:解:样本空间的样本点应该是甲、乙两袋中的样本点之积,也就是从甲袋中取一个球再从乙袋中取一球的所有取法,即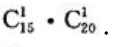 两球颜色相同的情况有三种,因此其样本点共有
两球颜色相同的情况有三种,因此其样本点共有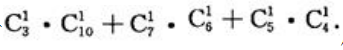 所以两球颜色相同的概率为
所以两球颜色相同的概率为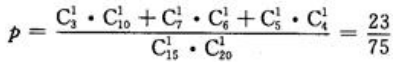
2、计算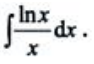
答 案:解:
填空题
1、若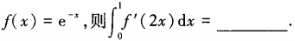
答 案: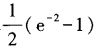
解 析:本题考查的知识点是积分变量的概念定积分的性质及定积分的计算。 
2、设 ,则
,则 ()
()
答 案: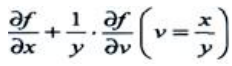
解 析:设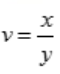 ,则z=f(x,v),则
,则z=f(x,v),则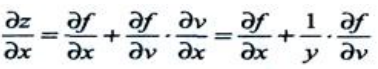
简答题
1、设z=z(x,y)是由方程x2+y2+z2=ez所确定的隐函数,求dz。
答 案:
2、设函数y=sin2x,求
答 案: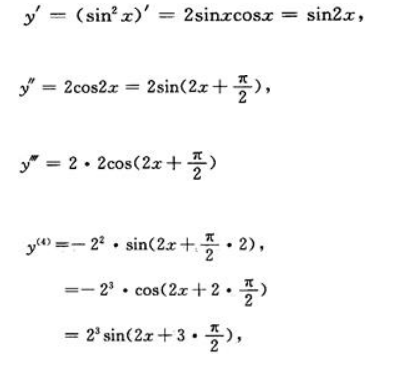 所以
所以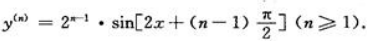
更多推荐

