单选题

1、下列各式的值为零的是（）。

• A：0⁰
• B：log₁1
• C：
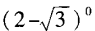
• D：log₂|-1|

答 案：D

解 析：0⁰和log₁1均没有意义，可排除（A）、（B），而（2-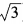）⁰=1。故选D。

2、若函数y=2^x-1+3的反函数的图像经过点P，则点P的坐标是（）。

• A：(1，2)
• B：(2，1)
• C：(2，5)
• D：(5，2)

答 案：D

解 析：反函数与原函数的x与y互换，原函数中，x＝2时，y＝5．故(5，2)为反函数图像上的点。答案为D。  

3、设log₅7＝m，log₂5＝n，则log₂7＝（）。

• A：
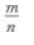
• B：
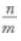
• C：m＋n
• D：m·n

答 案：D

解 析：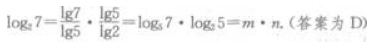

4、已知{i，j，k}是单位正交基底，a＝i＋j，b＝－i＋j－k，则a·b＝（）。

• A：-1
• B：1
• C：0
• D：2

答 案：C

解 析：a·b＝（1，1，0）·（－1，1，－1）＝1×（－1）＋1×1＋0×（－1）＝0。答案为C。  

主观题

1、计算。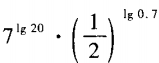  

答 案：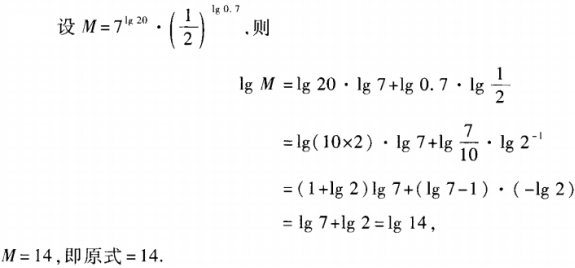

2、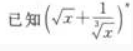 展开式的二项式系数之和比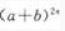展开式的二项式系数之和小240。 求：（1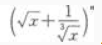）展开式的第3项；
（2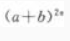）展开式的中间项。

答 案：

3、已知设△ABC的三边长为a、b、C，2sin²A=3（sin²B+sin²C）且cos2A+3cosA+3cos（B-C）=1，求证：a：b：c=：1：1。

答 案：因所证的是△ABC三边的比，所以可将题中角的关系式转化为边的关系式，需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin²A=3（sin²B+sin²C）…① 由正弦定理得，2a²=3（b²+c²）…②
∵cos2A+3cosA+3cos（B-C）=1
∴3[cosA+cos（B-C）]=1-cos2A.
∵A=180°-（B+C）
∴3[-cos（B+C）+cos（B-C）]=2sin²A. 由两角和与差的余弦公式得
6sinBsinB=2sin²A…③
由①③得，2sinBsinC=sin²B+sin²C.
sin²B-2sinBsinC+sin²C=0
（sinB-sinC）²=0
sinB= sinC.
由正弦定理得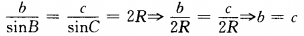

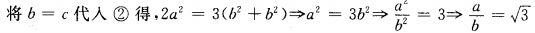
∴a：b=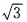：1
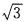于是a：b：c=：1：1。  

4、设a为实数，且tanα和tanβ是方程ax²+（2a-3）x+（a-2）=0的两个实根，求tan（α+β）的最小值。

答 案：由已知得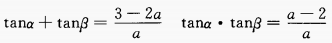

填空题

1、=______。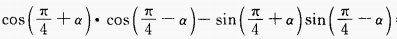  

答 案：0

解 析：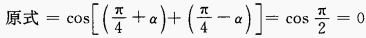

2、函数y=-x²+ax图像的对称轴为x=2，则a=______。  

答 案：4

解 析：本题主要考查的知识点为二次函数的性质 由题意，该函数图像的对称轴为