判断题

1、若，则。（）  

答 案：错

解 析：所以  

单选题

1、（）。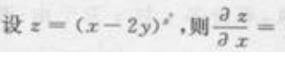  

• A：
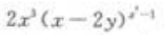
• B：
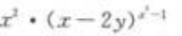
• C：
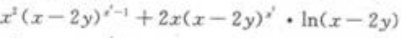
• D：

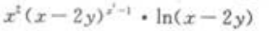
答 案：C

解 析：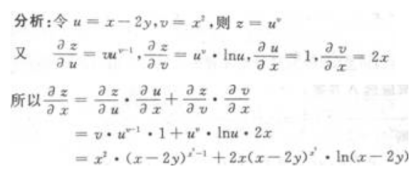

2、定积分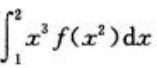等于（）

• A：
• B：
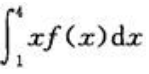
• C：
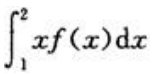
• D：

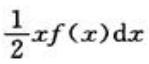
答 案：A

解 析：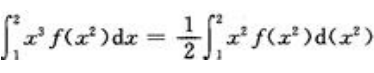

主观题

1、求由方程siny＋xe^y＝0确定的曲线在点（0，π）处的切线方程．

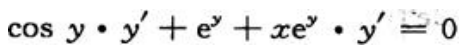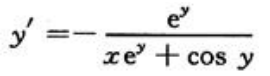答 案：解：方程两边对x求导得得所以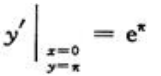,故所求切线方程为y－π＝e^π（x－0）,即e^πx－y＋π＝0

2、已知函数f(x)＝－x²＋2x．（1）求曲线y＝f(x)与x轴所围成的平面图形的面积S；
（2）求（1）中的平面图形绕x轴旋转一周所得旋转体的体积V．

答 案：解：（1）由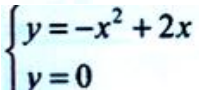得曲线与x轴交点坐标为（0，0），（2，0）．（2）

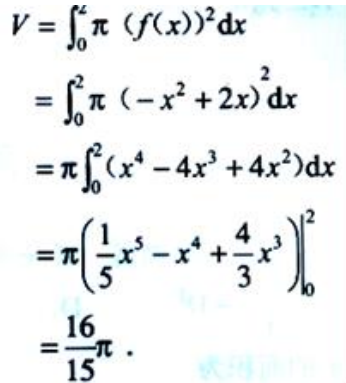
填空题

1、（）．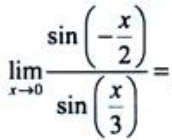

答 案：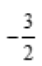

解 析：由等价无穷小知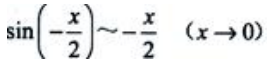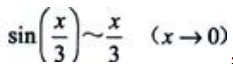，，所以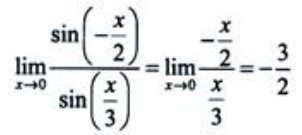

2、（）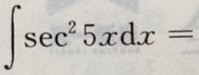

答 案：

解 析：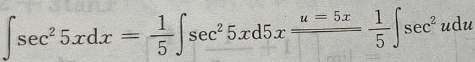

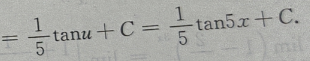
简答题

1、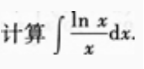  

答 案：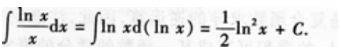

2、求函数的单调区间、极值及函数曲线的凸凹性区间、拐点和渐近线.

答 案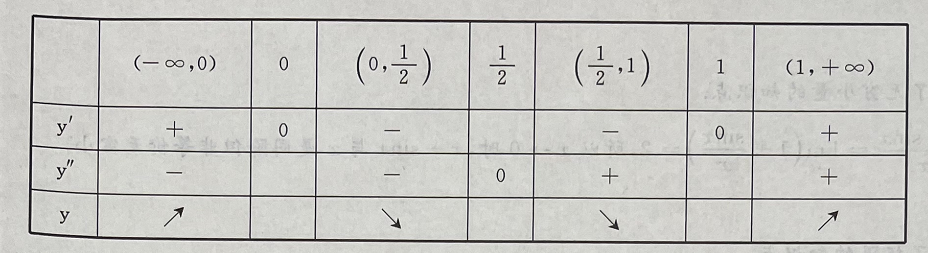：所以函数y的单调增区间为单调减区间为（0,1）；函数y的凸区间为凹区间为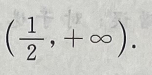故x=0时，函数有极大值0，x=1时，函数有极小值-1，且点为拐点，因不存在，且没有无意义的点，故函数没有渐近线。