2024年高职单招《数学(中职)》每日一练试题09月29日
精选习题
2024-09-29
15:55:37
收藏
单选题
1、函数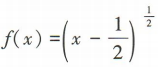 的定义域是()
的定义域是()
- A:
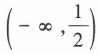
- B:
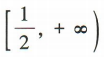
- C:
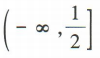
- D:
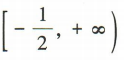
答 案:B
解 析:因为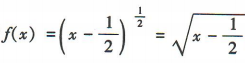 ,所以
,所以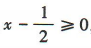 ,所以
,所以 ,所以f(x)的定义域为
,所以f(x)的定义域为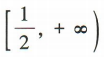 。
。
2、若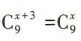 ,则x的值为()
,则x的值为()
- A:3
- B:6
- C:9
- D:3或6
答 案:A
解 析:因为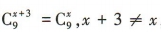 ,所以x+3+x=9,解得x=3.
,所以x+3+x=9,解得x=3.
3、已知平面直角坐标系上的两点A(-1,1),B(3,2),则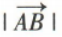 =()
=()
- A:√2
- B:3
- C:√6
- D:√17
答 案:D
解 析:由题意得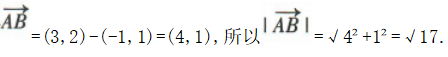
4、已知集合M={0,1,2,3,4},N={3,4,5},则下列结论正确的是
- A:
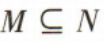
- B:
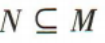
- C:M∩N={3,4}
- D:M∪N={0,1,2,5}
答 案:C
解 析:因为M={0,1,2,3,4},N={3,4,5},所以M不包含N,N不包含M,M∩N={3,4},M∪N={0,1,2,3,4,5},故选C
填空题
1、已知|a|=2,|b|=4,a·b=-4,则向量a与b的夹角为()
答 案:5
解 析:
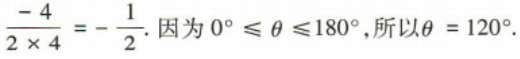
2、若函数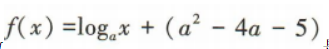 是对数函数,则a=()
是对数函数,则a=()
答 案:5
解 析: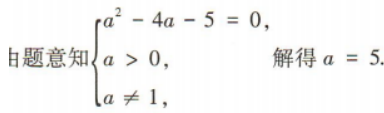
3、已知球的直径为2,则该球的体积是()
答 案: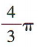
解 析:易得球的半径为1,故球的体积为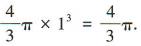
4、若(x-1)n的展开式中x2的系数是-10,则n的值为()
答 案:5
解 析:因为(x-1)n的展开式中x2的系数是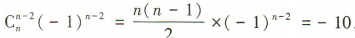 ,所以n= 5.
,所以n= 5.
简答题
1、如图,正方体ABCD-A1B1C1D1的棱长为 2.(1)证明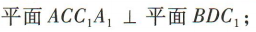
(2)求 AD1与 BD 所成角的大小.
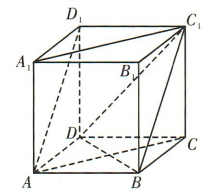
答 案:(1)在正方体ABCD-A1B1C1D1中,易得 又
又
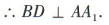 ∵四边形 ABCD 是正方形,
∵四边形 ABCD 是正方形,
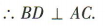 又
又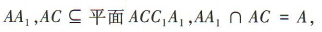
 又
又
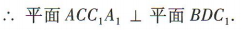 (2)在正方体ABCD-A1B1C1D1中,易得A1D1// BC,
∴
(2)在正方体ABCD-A1B1C1D1中,易得A1D1// BC,
∴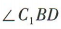 即AD1与BD所成的角,
易知C1B=BD=C1D=
即AD1与BD所成的角,
易知C1B=BD=C1D= ∴
∴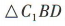 为等边三角形,
为等边三角形,
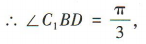 ∴AD1与BD所成的角为
∴AD1与BD所成的角为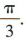
2、已知等差数列{an}的前n项和为Sn且S7=28,S15=120
(1)求数列{an}的首项a1和公差d;
(2)证明数列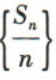 是等差数列,并求出
是等差数列,并求出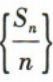 的前n项和Tn
的前n项和Tn
答 案: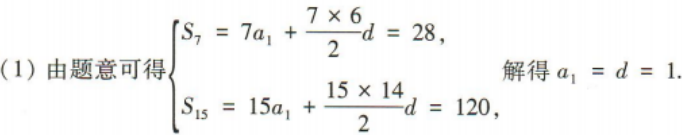
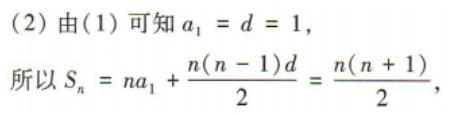
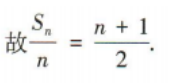
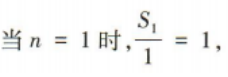
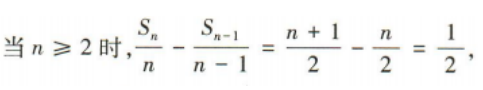

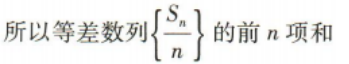
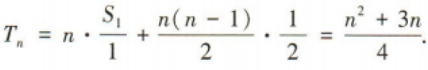
更多推荐

