2024年成考专升本《高等数学一》每日一练试题09月28日
精选习题
2024-09-28
11:30:18
收藏
单选题
1、设曲线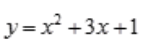 上某点处的切线方程为y=mx,则m的值可能是()。
上某点处的切线方程为y=mx,则m的值可能是()。
- A:0
- B:1
- C:2
- D:3
答 案:B
解 析: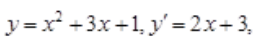 又曲线
又曲线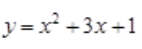 上某点处的切线方程为y=mx,设该点为
上某点处的切线方程为y=mx,设该点为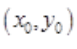 ,则有
,则有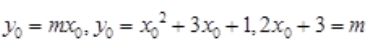 ,解得m=1或5。
,解得m=1或5。
2、下列命题中正确的有()。
- A:

- B:

- C:
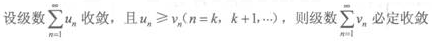
- D:

答 案:B
解 析:

3、 =()。
=()。
- A:0
- B:
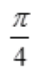
- C:arctanx
- D:

答 案:A
解 析:当定积分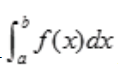 存在时,它表示一个常数值,常数的导数等于零。
存在时,它表示一个常数值,常数的导数等于零。
主观题
1、求微分方程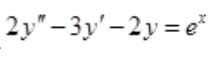 的通解。
的通解。
答 案:解: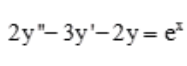 的特征值方程为
的特征值方程为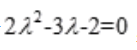 ,则
,则 ;故齐次微分方程的通解为
;故齐次微分方程的通解为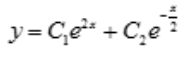 。由题意设原微分方程的特解为
。由题意设原微分方程的特解为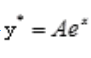 ,则有
,则有 ,得
,得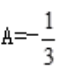 。即微分方程的通解为
。即微分方程的通解为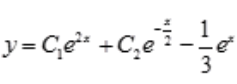 。
。
2、计算二重积分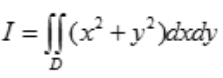 ,其中D是x2+y2≤1,x≥0,y≥0所围的平面区域.
,其中D是x2+y2≤1,x≥0,y≥0所围的平面区域.
答 案:解:D的图形见下图中阴影部分。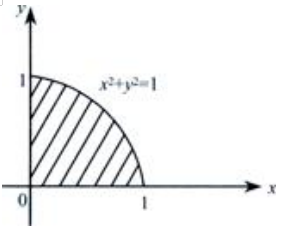 在极坐标系下D满足0≤
在极坐标系下D满足0≤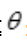 ≤
≤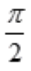 ,0≤r≤1,且x2+y2=(rcos
,0≤r≤1,且x2+y2=(rcos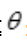 )2+(rsin
)2+(rsin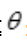 )2=r2,故
)2=r2,故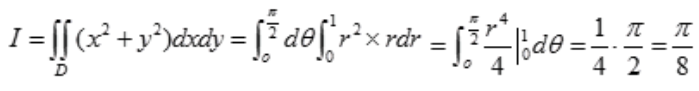 。
。
3、计算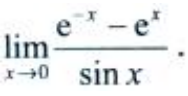
答 案:解:利用洛必达法则,得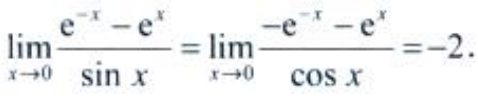
填空题
1、二阶常系数齐次微分方程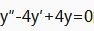 的通解为_____。
的通解为_____。
答 案:
解 析:


2、交换二次积分的积分次序,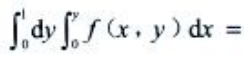 ()。
()。
答 案:
解 析:由题设有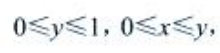 从而
从而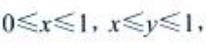 故交换次序后二次积分为
故交换次序后二次积分为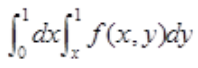 。
。
3、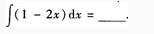
答 案:
解 析:
简答题
1、求函数f(x)=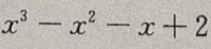 的单调区间。
的单调区间。
答 案: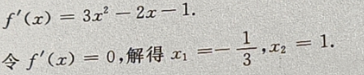
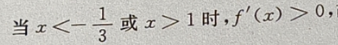
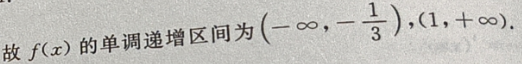


更多推荐

