2024年成考专升本《高等数学二》每日一练试题09月27日
精选习题
2024-09-27
11:30:15
收藏
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、设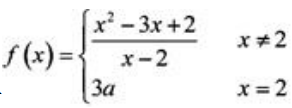 为连续函数,则a=().
为连续函数,则a=().
- A:
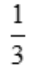
- B:
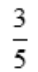
- C:2
- D:1
答 案:A
解 析:因为f(x)在x=2连续,所以
 故a=
故a=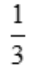 .
.
2、已知函数y=f(x)在实数集上恒有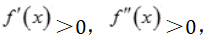 则曲线y=f(x)的图象( ).
则曲线y=f(x)的图象( ).
- A:单调上升且上凹
- B:单调下降且上凹
- C:单调上升且上凸
- D:单调下降且上凸
答 案:A
解 析: 故单调上升; 令
故单调上升; 令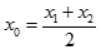 ,即
,即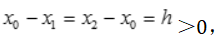 分别在
分别在 取
取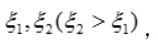
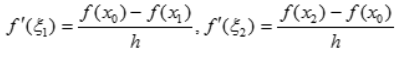 ,则
,则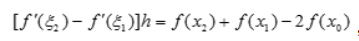
 可得
可得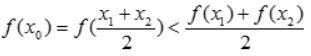 ,故函数上为凹。
,故函数上为凹。
主观题
1、求由方程siny+xey=0确定的曲线在点(0,π)处的切线方程.
答 案:解:方程两边对x求导得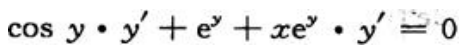 得
得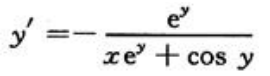 所以
所以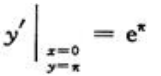 ,故所求切线方程为y-π=eπ(x-0),即eπx-y+π=0
,故所求切线方程为y-π=eπ(x-0),即eπx-y+π=0
2、求二元函数 的极值.
的极值.
答 案:解:令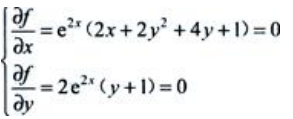 解得驻点
解得驻点 A=
A=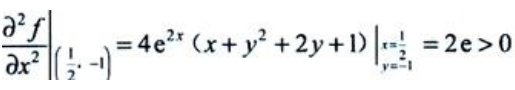 ,
, ,
,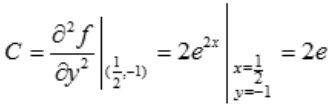 ,
, ,且A>0.所以在点
,且A>0.所以在点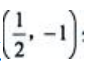 处函数f(x,y)取极小值,极小值为
处函数f(x,y)取极小值,极小值为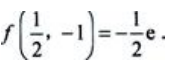
填空题
1、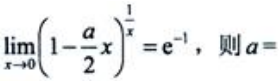 ().
().
答 案:2
解 析: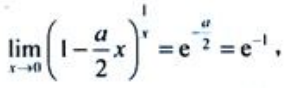 所以a=2.
所以a=2.
2、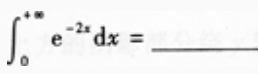 。
。
答 案: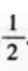
解 析: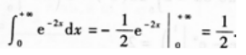
简答题
1、计算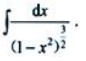
答 案:设x=sint,dx=costdt, 所以
2、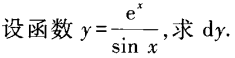
答 案:本题主要考查商的导数计算。 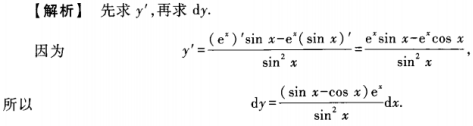
更多推荐

