单选题

1、设直线l方程为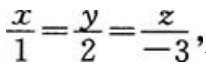：平面π与它垂直，则下列说法正确的是（）。

• A：直线l的方向向量与平面π的法向量垂直
• B：直线l的方向向量与平面π的法向量平行
• C：平面π的法向量是{1，2，3）
• D：直线l不经过原点

答 案：B

解 析：平面π与直线l垂直，可知直线l的方向向量与平面π的法向量平行。

2、（）。  

• A：发散
• B：条件收敛
• C：绝对收敛
• D：无法判定敛散性

答 案：C

解 析：收敛，所以选C。

3、（）。  

• A：x=-2
• B：x=1
• C：x=2
• D：x=3

答 案：B

解 析：所给级数为不缺项情形，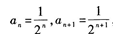  

主观题

1、求幂级数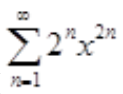的收敛区间（不考虑端点）。

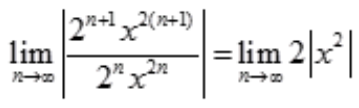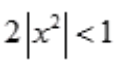答 案：解：，由可解得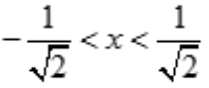，故所给级数收敛区间为。

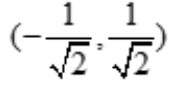2、求二元函数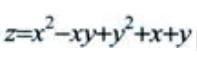的极值。

答 案：解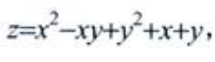：则由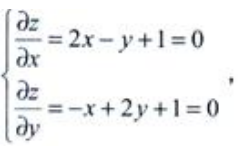点P（－1，1）为唯一驻点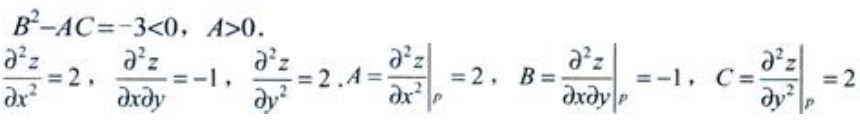，因此点（－1，－1）为z的极小值点，极小值为－1。

3、设函数f（x）＝x-lnx，求f（x）的单调增区间．

答 案：解：函数f（x）的定义域为（0，＋∞）。令y＝f（x），则令y'＝0，解得x＝1。当0＜x＜1时，y'＜0；当x＞1时，y'＞0。
因此函数f（x）的单调增区间为（1，＋∞）。

填空题

1、过点M₀（0，0，0）且与直线平行的直线方程为（）。

答 案：

解 析：所给直线的方向向量为（1，2，－1）．所求直线与已给直线平行，则可取所求直线方向向量为（1，2，－1）．由于所求直线过原点（0，0，0），由直线的点向式方程可知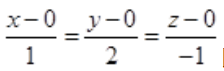即为所求直线方程。

2、过点M₀（1，0，-1）且与直线垂直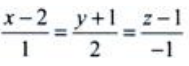的平面方程为（）。

答 案：

解 析：所求平面与已知直线垂直，则平面的法线向量n必定与直线的方向向量s＝（1，2，－1）平行，可取n＝（1，2，－1），又平面过点（1，0，－1），由平面的点法式方程可知所求平面方程为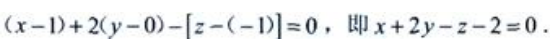

3、过点M（1，2，－1）且与平面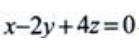垂直的直线方程为（）。

答 案：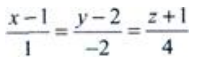

解 析：由于直线与平面x－2y＋4z＝0垂直，可取直线方向向量为（1，－2，4），因此所求直线方程为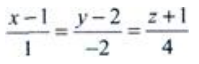

简答题

1、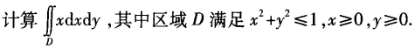  

答 案：积分区域D如图2-1所示。 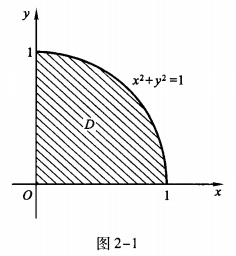解法1利用极坐标系。  

解 析：本题考查的知识点为计算二重积分；选择积分次序或利用极坐标计算。