单选题

1、圆C1：x²+y²=1与圆C2：x²+y²-4x=0的位置关系是（）。  

• A：外切
• B：内切
• C：相交
• D：相离

答 案：C

2、袋中有6个球，其中4个红球，2个白球，从中随机取出2个球，则这2个球都为红球的概率为（）

• A：
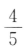
• B：
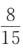
• C：
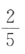
• D：

答 案：C

解 析：两个球都是红球的概率为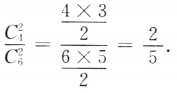

3、△ABC中，已知AC=12，∠A=30°，∠B=120°，则BC=（）

• A：
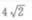
• B：
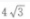
• C：
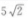
• D：

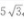
答 案：B

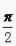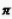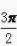4、cos+cos（-）+cot+sin+tan=（）。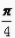

• A：2
• B：1
• C：-2
• D：-1

答 案：D

主观题

1、设全集U=R，集合A={x｜-5＜x＜5}，B={x｜0≤x≤7}，求CUA∩B．

答 案：解：全集U=R，A={x｜-5＜x＜5}，B=｛X｜0≤x≤7}，因为CuA={x｜x≤-5或x≥5}，所以CuA∩B={x｜x≤-5或x≥5}N{x｜0≤x≤7}={x｜5≤x≤7}，如图1—10所示。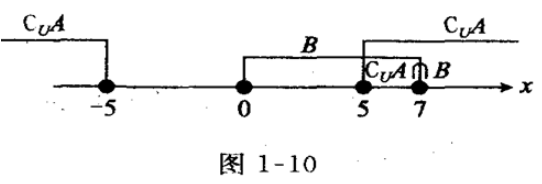

2、设函数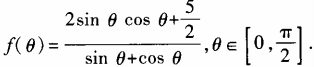 （1）求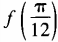；（2）求函数f（θ）最小值。

答 案：

3、在△ABC中，已知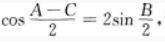证明a，b，c成等差数列。

答 案： 考点 本题主要考查三角函数的恒等变换以及积化和差公式的应用，积化和差有一定难度，请考生注意．

4、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.
(I）求l与C的准线的交点坐标；
(II）求|AB|．

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由得设A（x1,y1）.B（x2,y2），则因此

填空题

1、平面内有10个点，任何三点都不在同一直线上，问能连成______条不同的直线。  

答 案：45

2、“a=0，且b=0”是“a²+b²=0的”______。  

答 案：充要条件