2024年成考专升本《高等数学二》每日一练试题09月17日
精选习题
2024-09-17
11:24:28
收藏
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、二元函数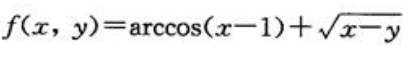 的定义域为().
的定义域为().
- A:0≤x≤2,y≤2
- B:0≤x≤2,x≥y
- C:0≤x≤2,y≤0
- D:0<x<2,x>y
答 案:B
解 析:由题可知有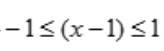 且
且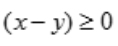 ,解不等式得
,解不等式得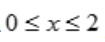 且
且 .
.
2、
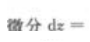 ()。
()。
- A:
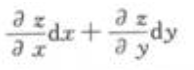
- B:
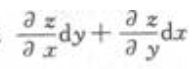
- C:
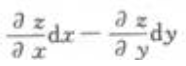
- D:
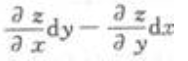
答 案:A
解 析:分析:由全微分存在定理知,应选择A。
主观题
1、设 ,其中f为可微函数.证明:
,其中f为可微函数.证明: .
.
答 案:证:因为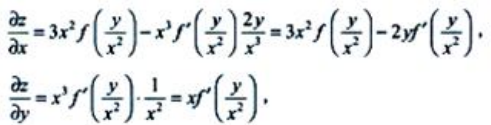 所以
所以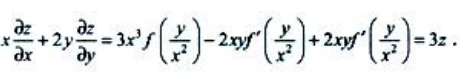
2、求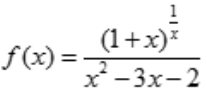 的间断点,并指出类型.
的间断点,并指出类型.
答 案:解:因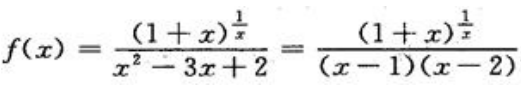 ,故x=0,x=1,x=2是f(x)的间断点,又
,故x=0,x=1,x=2是f(x)的间断点,又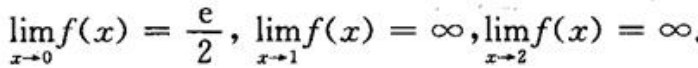 又因,f(0)、f(1)、f(2)都不存在,所以x=0是f(x)的第一类间断点(可去间断点);x=1,x=2是,f(x)的第二类间断点(无穷间断点).
又因,f(0)、f(1)、f(2)都不存在,所以x=0是f(x)的第一类间断点(可去间断点);x=1,x=2是,f(x)的第二类间断点(无穷间断点).
填空题
1、设函数f(x)=e2x,则f(n)(0)=()
答 案:2n
解 析:本题考查了高阶导数的知识点. 因为f(n)(x)=2ne2x,故f(n)(0)=2n
2、 ______。
______。
答 案:0
解 析:因为x3cosx是奇函数。
简答题
1、求函数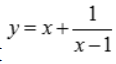 的单调区间、极值及凹凸区间.
的单调区间、极值及凹凸区间.
答 案:函数定义域为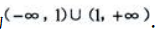 求导得
求导得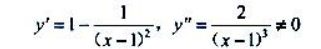 令
令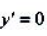 得
得 列表得
列表得 函数
函数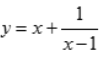 的单调增加区间为
的单调增加区间为 单调减少区间为
单调减少区间为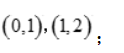
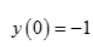 为极大值,
为极大值, 极小值;凸区间为
极小值;凸区间为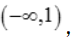 凹区间为
凹区间为 。
。
2、要做一个容积为V立方米的密闭圆柱形容器,两底面材料的价格为每平方米a元,侧面材料的价格为每平方米b元,问圆柱形容器的底面半径与高的比等于多少时,造价最低?
答 案:设底面半径和高分别为r,h,则造价函数L=2aπr2+2bπrh,且πr2,且πr2h=V 将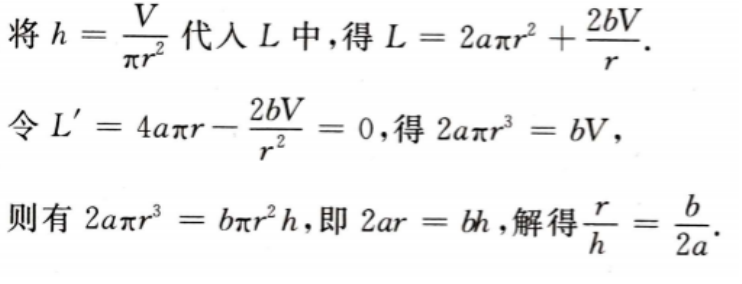 由实际问题的意义知,当底面半径与高的比为
由实际问题的意义知,当底面半径与高的比为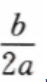 时,造价最低.
时,造价最低.
更多推荐

