2024年成考专升本《高等数学二》每日一练试题09月10日
精选习题
2024-09-10
11:28:39
收藏
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、设f(x)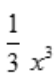 =-x,则x=1为f(x)在[-2,2]上的().
=-x,则x=1为f(x)在[-2,2]上的().
- A:极小值点,但不是最小值点
- B:极小值点,也是最小值点
- C:极大值点,但不是最大值点
- D:极大值点,也是最大值点
答 案:B
解 析: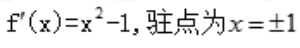 ,
,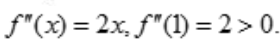 所以x=1为极小值点.又
所以x=1为极小值点.又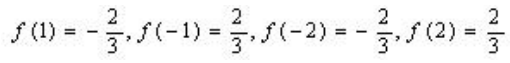 ,所以x=1为极小值点,也是最小值点.
,所以x=1为极小值点,也是最小值点.
2、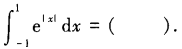
- A:0
- B:e-1
- C:2(e-1)
- D:
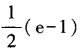
答 案:C
解 析:本题考查的知识点是奇、偶函数在对称区间上的定积分计算。 注意到被积函数是偶函数的特性,可知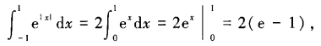 所以选C。
所以选C。
主观题
1、一批零件中有10个合格品和2个废品,安装机器时,从这批零件中任取一个,如果每次取出废品后不再放回,用X表示在取得合格品以前已取出的废品数,求:(1)随机变量X的分布列;
(2)随机变量X的分布函数.
答 案:解:(1)由题意知,随机变量X的可能值是0,1,2,且有 随机变量x的分布列为
随机变量x的分布列为 (2)随机变量X的分布函数为
(2)随机变量X的分布函数为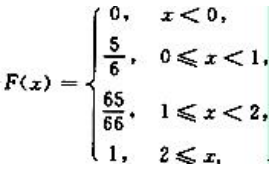
2、计算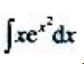 .
.
答 案:解: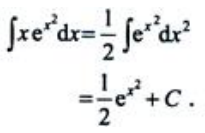
填空题
1、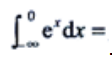 ().
().
答 案:1
解 析: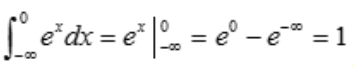 .
.
2、若 存在,且
存在,且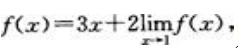 则
则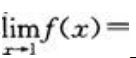 ().
().
答 案:-3
解 析:设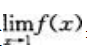 =A,对
=A,对 两边求x=1处的极限得A=3+2A,解得A=-3,即
两边求x=1处的极限得A=3+2A,解得A=-3,即 =-3.
=-3.
简答题
1、
答 案: 。
。 
2、设函数f(x,y)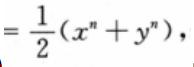 n为大于1的整数,求在条件x+y=c下f(x,y)得最小值,其中x>0,y>0,c为正常数。
n为大于1的整数,求在条件x+y=c下f(x,y)得最小值,其中x>0,y>0,c为正常数。
答 案: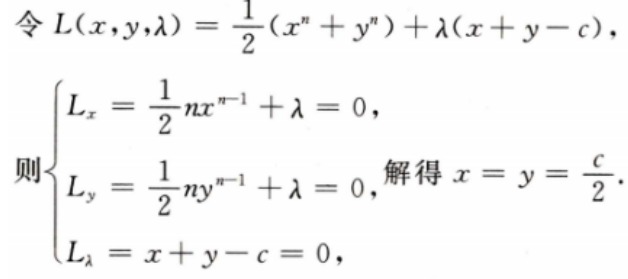 由实际问题的意义知当x=y=
由实际问题的意义知当x=y=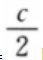 时,f(x,y)取得最小值
时,f(x,y)取得最小值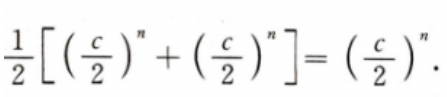
更多推荐

