单选题

1、函数y=2sinxcosx的最小正周期是（）  

• A：
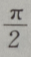
• B：
• C：
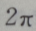
• D：

答 案：D

解 析：y=2sinxcosx=sin2x，故其最小正周期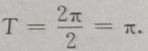

2、如果函数y=kx+b的图像经过A（1，2）和B（0，1），则k=（）。  

• A：-5
• B：1
• C：2
• D：5

答 案：B

3、下列函数中，为奇函数的是（）

• A：y=cos²x
• B：y=sinx
• C：y=2^-x
• D：y=x+1

答 案：B

解 析：当f(-x)=-f(x)时，函数f(x)是奇函数，四个选项中只有选项B符合，故选B选项．

4、若a，b，c分别表示△ABC的顶点A，B，C所对的边长，且（a+b+c）（a+b-c）=3ab，cos（A+B）=（）。

• A：
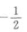
• B：
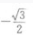
• C：
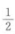
• D：

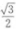
答 案：A

主观题

1、已知x+x^-1=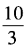，求x²+x^-2的值。  

答 案：由已知，得

2、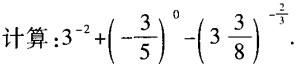  

答 案：

3、设函数f(x)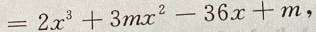且f'(-1)=-36 (Ⅰ)求m (Ⅱ)求f(x)的单调区间

答 案：(Ⅰ)由已知得f'=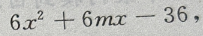 又由f'(-1)=-36得 6-6m-36=-36 故m=1. (Ⅱ)由(Ⅰ)得f'(x)=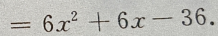 令f'(x)=0，解得 当x<-3时，f'(x)>0; 当-32时，f'(x)>0; 故f(x)的单调递减区间为(-3,2)，f(x)的单调递增区间为(-∞,-3),(2,+∞)  

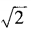4、已知a^m=，aⁿ=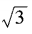，求a^3n-4m的值。  

答 案：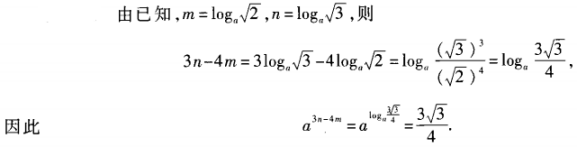

填空题

1、甲、乙、丙三位教师担任6个班的课，如果每人任选两个班上课有______种不同的任课方法。  

答 案：90

2、“a=0，且b=0”是“a²+b²=0的”______。  

答 案：充要条件