单选题
1、设甲:二次不等式x2+px+q>0的解集为空集合;乙:△=p2-4q<0则()。
- A:甲是乙的必要条件,但不是乙的充分条件
- B:甲是乙的充分条件,但不是乙的必要条件
- C:甲不是乙的充分条件,也不是乙的必要条件
- D:甲是乙的充分必要条件
答 案:D
解 析:由于二次不等式x2+px+q>0的解集为空集合△=p2-4q<0,则甲是乙的充分必要条件(答案为 D)
2、过点P(2,3)且在两轴上截距相等的直线方程为()
- A:
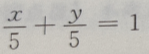
- B:
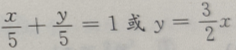
- C:x+y=5
- D:
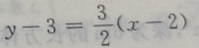
答 案:B
解 析:选项A中,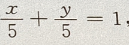 在x、y 轴上截距为 5.但答案不完整 所以选项B中有两个方程,
在x、y 轴上截距为 5.但答案不完整 所以选项B中有两个方程,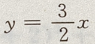 在x轴上横截距与y轴上的纵截距都为0,也是相等的
选项C,虽然过点(2,3),实质上与选项A相同.选项 D,转化为:
在x轴上横截距与y轴上的纵截距都为0,也是相等的
选项C,虽然过点(2,3),实质上与选项A相同.选项 D,转化为: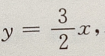 答案不完整
答案不完整
3、下列函数中,为增函数的是()。
- A:y=x3
- B:y=x2
- C:y=-x2
- D:y=-x3
答 案:A
解 析:本题主要考查的知识点为函数的单调性. 对于y=x3,y’=3x2≥0,故y=x3为增函数
4、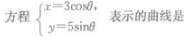 ()。
()。
- A:圆
- B:椭圆
- C:双曲线
- D:抛物线
答 案:B
解 析:消去参数,化曲线的参数方程为普通方程, 
主观题
1、已知x+x-1=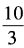 ,求x2+x-2的值。
,求x2+x-2的值。
答 案:由已知,得

2、已知抛物线C:y2=2px(p>0)的焦点到准线的距离为1。 (I)求C的方程; (Ⅱ)若A(1,m)(m>0)为C上一点,O为坐标原点,求C上另一点B的坐标,使得OA⊥OB
答 案:(I)由题意,该抛物线的焦点到准线的距离为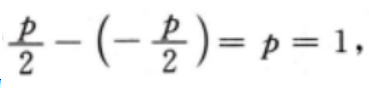 所以抛物线C的方程为
所以抛物线C的方程为 (Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得
(Ⅱ)因A(l,m)(m>0)为C上一点,故有m2=2,
可得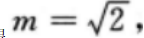 因此A点坐标为
因此A点坐标为 设B点坐标为
设B点坐标为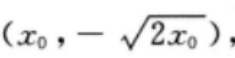 则
则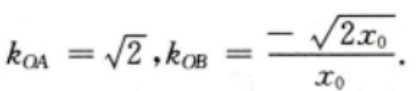 因为
因为 则有
则有 即
即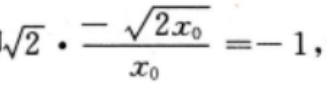 解得x0=4
所以B点的坐标为
解得x0=4
所以B点的坐标为
3、当自变量为何值时,函数y=2x3-3x2-12x+21有极值,其极值为多少?
答 案:y'=6x2-6x-12=6(x-2)(x+1) 当x<-1或x>2时,y>0,当-1
4、已知等差数列{an}中,a1+a2+a3=6,a2+a4+a5= 12求{an}的首项与公差。
答 案:因为{an}为等差数列,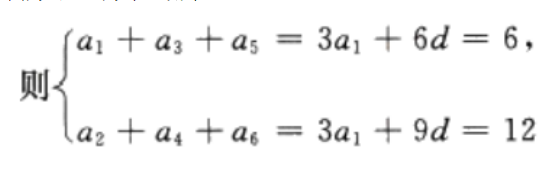
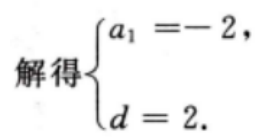
填空题
1、 的展开式是()
的展开式是()
答 案: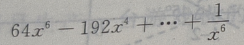
解 析: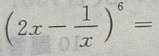
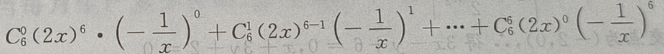

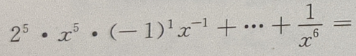
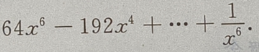
2、曲线y=在点(1,1)处的切线方程是______。
答 案:2x+y-3=0
解 析:本题主要考查的知识点为切线方程
由题意,该切线斜率,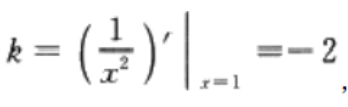 又过点(1,1),所以切线方程为y-1=-2(x-1)
又过点(1,1),所以切线方程为y-1=-2(x-1)

