单选题
1、 的展开式中,x2的系数为()
的展开式中,x2的系数为()
- A:20
- B:10
- C:5
- D:1
答 案:C
解 析:二项展开式的第二项为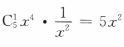 ,故展开式中的x2的系数为5.
,故展开式中的x2的系数为5.
2、若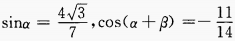 ,且α、β均为锐角,则β的值为()。
,且α、β均为锐角,则β的值为()。
- A:
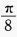
- B:
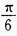
- C:
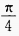
- D:
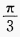
答 案:D
解 析:
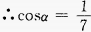
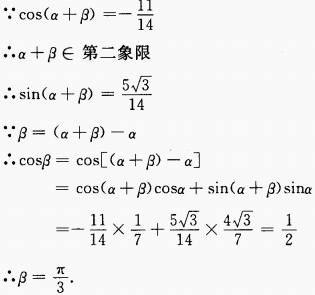
3、分别和两条异面直线AB、CD同时相交的两条直线AC、BD()。
- A:相交
- B:平行
- C:是异面直线
- D:垂直
答 案:C
4、已知偶函数y=f(x),在区间[a,b](0 答 案:B 解 析:由偶函数的性质:偶函数在[a,b]和[-b,-a]上有相反的单调性,可知,y=f(x)在区间[a,b](0 主观题 1、已知直线l的斜率为1,l过抛物线C: 答 案:(I)C的焦点为 2、已知设△ABC的三边长为a、b、C,2sin2A=3(sin2B+sin2C)且cos2A+3cosA+3cos(B-C)=1,求证:a:b:c= 答 案:因所证的是△ABC三边的比,所以可将题中角的关系式转化为边的关系式,需用正弦定理关于题中的余弦关系式可通过恒等变形化为正弦函数的关系式。 ∵2sin2A=3(sin2B+sin2C)…① 由正弦定理得,2a2=3(b2+c2)…② 3、已知A(1,4),B(3,8),C(4,10)。求证A、B、C三点共线。
答 案: 4、设 答 案: 填空题 1、点B(4,-5)按向量a平移后的对应点B0(-4,7),则a的坐标是______。
答 案:(-8,12) 解 析:由平移公式得-4=4+a1,7=-5+a2→a1=-8,a2=12 ∴a的坐标是(-8,12)。
2、函数y=x4-2x2+5,x∈[-2,2]上的最小值______,最大值______。 答 案:4;13 解 析:y=x4-2x2+5,y'=4x3-4x 的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
的焦点,且与C交于A,B两点.(I)求l与C的准线的交点坐标;
(II)求|AB|. ,准线为
,准线为 由题意得l的方程为
由题意得l的方程为 因此l与C的准线的交点坐标为
因此l与C的准线的交点坐标为 (II)由
(II)由 ,得
,得 设A(x1,y1),B(x2,y2),则
设A(x1,y1),B(x2,y2),则 因此
因此
 :1:1。
:1:1。
∵cos2A+3cosA+3cos(B-C)=1
∴3[cosA+cos(B-C)]=1-cos2A.
∵A=180°-(B+C)
∴3[-cos(B+C)+cos(B-C)]=2sin2A.
由两角和与差的余弦公式得
6sinBsinB=2sin2A…③
由①③得,2sinBsinC=sin2B+sin2C.
sin2B-2sinBsinC+sin2C=0
(sinB-sinC)2=0
sinB= sinC.
由正弦定理得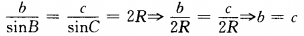
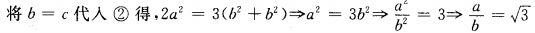
∴a:b=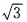 :1
:1
于是a:b:c=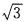 :1:1。
:1:1。
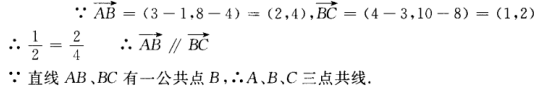
 (0<α<π),求tanα的值。
(0<α<π),求tanα的值。


