单选题

1、若向量a=（x，-2），b=（-2，1），且a//b，则x=（）。

• A：-4
• B：-1
• C：1
• D：4

答 案：D

2、（）。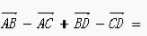

• A：
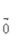
• B：
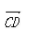
• C：
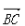
• D：

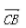
答 案：A

3、掷两颗骰子点数之和等于4的概率是（）。

• A：
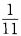
• B：
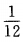
• C：
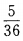
• D：

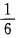
答 案：B

解 析：掷一对骰子的等可能结果共有n=36种，点数之和等于4的结果有1+3=4，3+1=4，2+2=4，故有m=3种，所以其概率为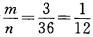故选B。  

4、在△ABC中，三边为a、b、c，∠B=60°，则的值是（）  

• A：大于零
• B：小于零
• C：等于零
• D：不能确定

答 案：C

解 析：由已知用余弦定理得：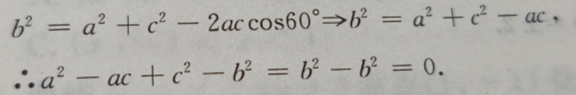  

主观题

1、设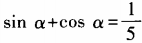（0＜α＜π），求tanα的值。  

答 案：

2、等差数列{an}的通项公式为an=3n-1，在{an}中，每相邻的两项之间插人三项，构成新的等差数列{bn}． (Ⅰ)求{bn}的通项公式； (Ⅱ)求{bn}前10项的和．

答 案： 考点本题主要考查等差数列的通项公式和前n项和公式的运用，是成人高考常见题型．

3、设函数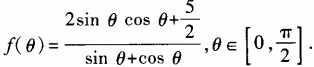 （1）求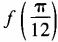；（2）求函数f（θ）最小值。

答 案：

4、已知函数f（x）=（x-4）（x2-a）。（I）求f’（x）；
（Ⅱ）若f’（-1）=8，求f（x）在区间[0，4]的最大值与最小值。

答 案：(I)f'(x) =(x-4)'(x²-a)+(x-4)(x²-a)’ =x²-a+2x(x-4) =3x²-8x-a. (Ⅱ)由于f’(-1)=3+8-a=8,得a=3. 令f'(x)=3x²-8x-3=0,解得x1=3，（舍去）又f（0）=12，f（3）=-6，f（4）=0所以在区间[0，4]上函数最大值为12，最小值为-6

填空题

1、袋中装有3个白球，2个红球，从中任取2个球，取到2个都是红球的概率是______。  

答 案：

解 析：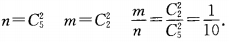

2、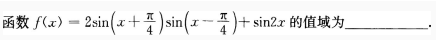  

答 案：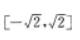

解 析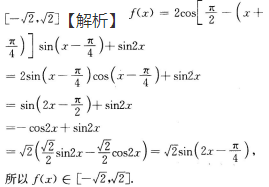： 【考点指要】本题主要考查三角函数的最大值、最小值及值域的求法，解题时需要灵活运用诱导公式、二倍角公式以及辅助角公式，当函数可以化