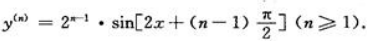判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、设函数z=xey,则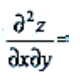 ().
().
答 案:B
解 析: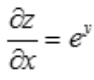 ,
,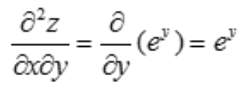 .
.
2、设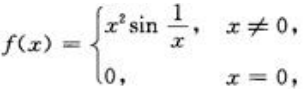 则f(x)在点x=0处().
则f(x)在点x=0处().
 =0
=0 =1
=1答 案:A
解 析:因为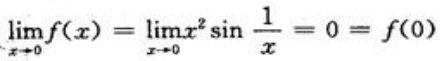 ,所以,f(x)在x=0处连续;又
,所以,f(x)在x=0处连续;又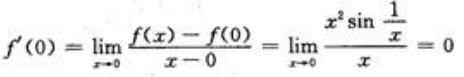 所以f(x)在点x=0处可导且
所以f(x)在点x=0处可导且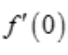 =0.
=0.
主观题
1、计算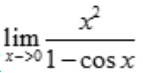 .
.
答 案:解: .
.
2、计算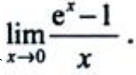
答 案:解:这是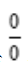 型极限,可以使用洛必达法则
型极限,可以使用洛必达法则
填空题
1、设函数f(x)在x=2处连续,且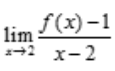 存在,则f(2)=().
存在,则f(2)=().
答 案:1
解 析:因为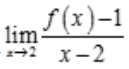 存在,所以
存在,所以 ,即
,即 .因为f(x)在x=2处连续,所以f(2)=1.
.因为f(x)在x=2处连续,所以f(2)=1.
2、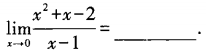
答 案:2
解 析:
简答题
1、已知函数f(x)=ax3-bx2+cx在区间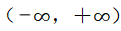 内是奇函数,且当x=1时,f(x)有极小值
内是奇函数,且当x=1时,f(x)有极小值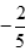 ,求另一个极值及此曲线的拐点.
,求另一个极值及此曲线的拐点.
答 案:f(x)=ax3-bx2+cx,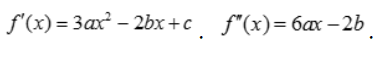 由于f(x)是奇函数,则必有x2的系数为0,即b=0.
由于f(x)是奇函数,则必有x2的系数为0,即b=0.
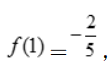 即a+c=
即a+c=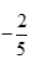 ,
,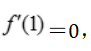 得3a+c=0.解得a=
得3a+c=0.解得a=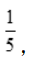 c=
c= 此时
此时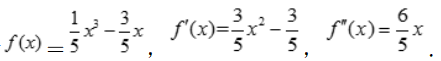 令
令 得
得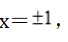
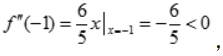 所以
所以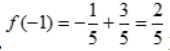 为极大值,
为极大值,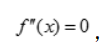 得x=0,x<0时,
得x=0,x<0时,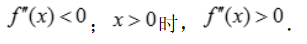 所以(0,0)为曲线的拐点.
所以(0,0)为曲线的拐点.
2、设函数y=sin2x,求
答 案: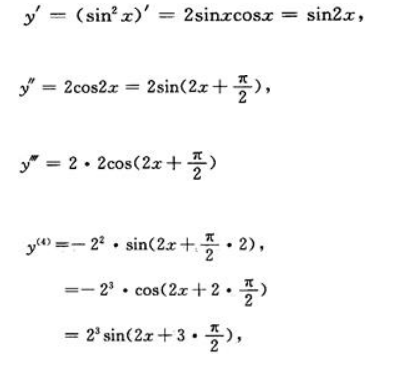 所以
所以