2024年成考专升本《高等数学二》每日一练试题08月24日
考试问答
2024-08-24
11:22:10
收藏
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、如果函数y=f(x)在x0处满足 ,则().
,则().
- A:x0是驻点
- B:x0不是驻点
- C:x0是极值点
- D:x0不是极值点
答 案:A
解 析:驻点的定义:函数的一阶导数为0的点的x的值,驻点可以划分函数的单调区间.可导函数f(x)的极值点一定是它的驻点;但反过来,函数的驻点不一定是极值点.例如函数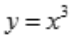 ,x=0是函数的驻点,但不是极值点.
,x=0是函数的驻点,但不是极值点.
2、设函数f(x)=lnx-x,则f(x)=()。
- A:x
- B:x-1
- C:
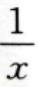
- D:
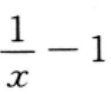
答 案:D
解 析:本题考查了导数运算的知识点 f’(x)=(lnx-x)’=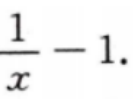
主观题
1、计算
答 案:解: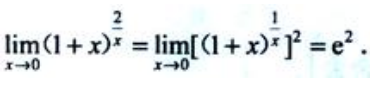
2、已知离散型随机变量X的概率分布为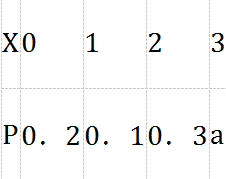 (1)求常数a;
(1)求常数a;
(2)求X的数学期望EX和方差DX.
答 案:解:(1)因为0.2+0.1+0.3+a=1,所以a=0.4;(2)EX=0×0.2+1×0.1+2×0.3+3×0.4=1.9;DX=(0-1.9)2×0.2+(1-1.9)2×0.1+(2-1.9)2×0.3+(3-1.9)2×0.4=1.29.
填空题
1、设函数y=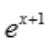 ,则y''=().
,则y''=().
答 案:ex+1
解 析: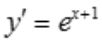 ,
,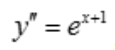 .
.
2、设函数z=ln(x+y),则全微分dz=________。
答 案: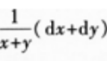
解 析: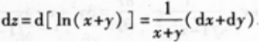
简答题
1、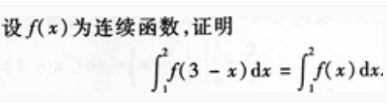
答 案:设3-x=t,则4dx=-dt。 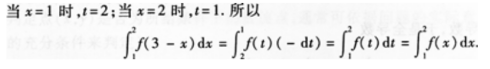
2、要做一个容积为V立方米的密闭圆柱形容器,两底面材料的价格为每平方米a元,侧面材料的价格为每平方米b元,问圆柱形容器的底面半径与高的比等于多少时,造价最低?
答 案:设底面半径和高分别为r,h,则造价函数L=2aπr2+2bπrh,且πr2,且πr2h=V 将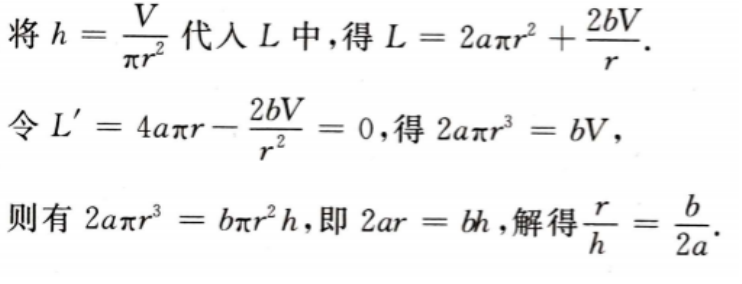 由实际问题的意义知,当底面半径与高的比为
由实际问题的意义知,当底面半径与高的比为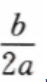 时,造价最低.
时,造价最低.
更多推荐

