2024年成考专升本《高等数学二》每日一练试题08月23日
精选习题
2024-08-23
11:26:13
收藏
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、已知f(x)=x+ex,g(x)=lnx,则f[g’(x)]等于()。
- A:
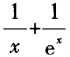
- B:
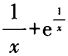
- C:
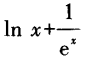
- D:
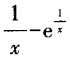
答 案:B
解 析:本题考查的知识点是复合函数的概念及其求导计算。 本题的关键是正确写出复合函数f[g’(x)]的表达式。根据函数概念可知: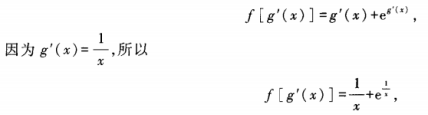
故选B。
2、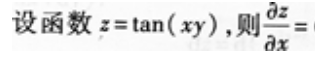 ()。
()。
- A:
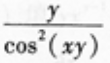
- B:
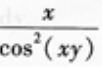
- C:
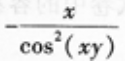
- D:
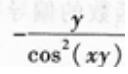
答 案:A
主观题
1、当 .
.
答 案:证:设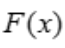 =ex-x-1,
=ex-x-1,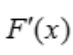 =ex-1.当x<0时,
=ex-1.当x<0时,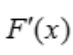 <0,F(x)单调递减,所以当x<0时,F(x)>F(0)=0,即ex-x-1>0,得ex>1+x.
<0,F(x)单调递减,所以当x<0时,F(x)>F(0)=0,即ex-x-1>0,得ex>1+x.
2、若f(x)的一个原函数为xsinx,求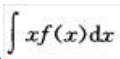 .
.
答 案:解:因为f(x)的一个原函数为xsinx,所以 因此
因此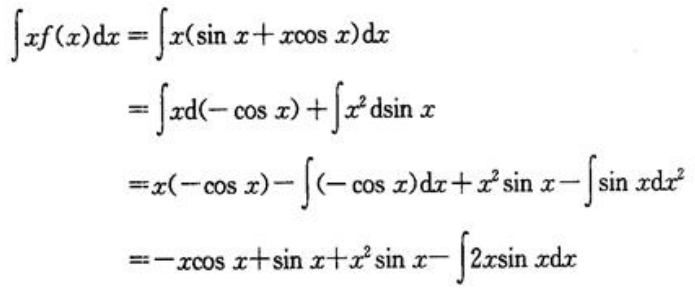
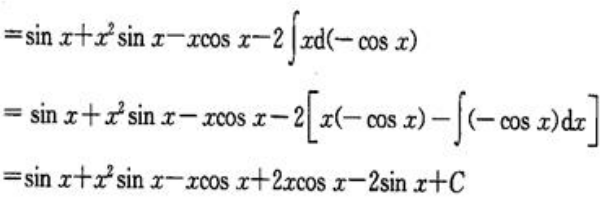
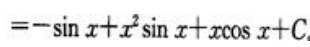 .
.
填空题
1、若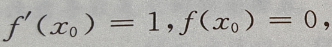 则
则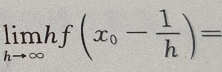
答 案:-1
解 析:
 注:注意导数定义的结构特点.
注:注意导数定义的结构特点.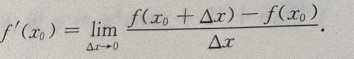
2、设函数y=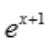 ,则y''=().
,则y''=().
答 案:ex+1
解 析: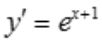 ,
,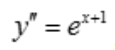 .
.
简答题
1、求函数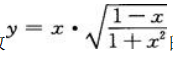 的倒数。
的倒数。
答 案:等式两边同时取对数得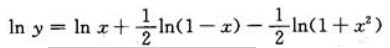 方程两边同时对x求导有
方程两边同时对x求导有 故
故
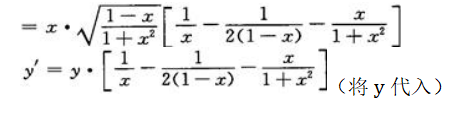
2、求函数ƒ(x,y)=x2+y2在条件2x+3y=1下的极值
答 案:解设F(x,y,λ)=x2+y2+λ(2x+3y-1), 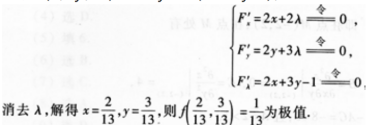
更多推荐

