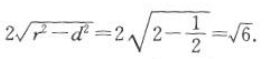判断题

1、已知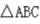三边长分别为3，5，7，则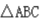是锐角三角形。（）  

答 案：错

解 析：因为△ABC的三条边长分别为3、5、7，由余弦定理b²=a²+c²-2accosB，即7²=5²+3²-2×5×3cosB，cosB=-，所以B为钝角．三角形是钝角三角形．

2、若不等式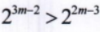成立，则实数m<-1。（）  

答 案：错

解 析：想要不等式成立，肯定是3m-2>2m-3。解开不等式，m＞-1

单选题

1、已知sin35°=cosα，则α为（）  

• A：35°
• B：55°
• C：75°
• D：65°

答 案：B

解 析：∵sin35°=cosα，∴α=90°-35°=55°。故选B。根据锐角三角函数的概念，可以证明：一个角的正弦值等于它的余角的余弦值。

2、下列抛物线中，其方程形式为y²=2px（p>0）的是（）  

• A：
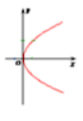
• B：
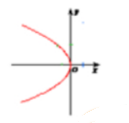
• C：
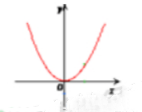
• D：

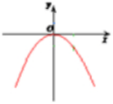
答 案：A

解 析：根据方程式可得其图像关于x轴对称，且x≥0，故可得该抛物线对称轴为x轴，开口向右

多选题

1、已知等差数列{a_n}的前n项和为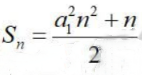，公差为d，则（）  

• A：a₁=1
• B：d=1
• C：2S_n-a_n=1+3+5+...+(2n-1)
• D：

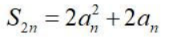
答 案：ABC

2、已知等差数列{a_n}的前n项和为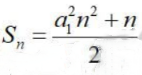，公差为d，则（）  

• A：a₁=1
• B：d=1
• C：
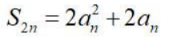
• D：2S_n-a_n=1+3+5+...+(2n-1)

答 案：ABD

主观题

1、已知函数f(x)=log₃(3x—1).(1)求函数f(x)的定义域；
(2)若f(x)<1,求x的取值范围.

答 案：(1)根据题意可得，3x-1>0,解得所以函数f(x)的定义域是(2)因为f(x)=log₃(3x-1)<1=log₃3,f(x)为定义域上的增函数，所以O<3x-1<3,解得所以x的取值范围是

2、已知等差数列{an}的前n项和S_n且S₅=35,S₈=104.
(1)求数列{an}的通项公式；
(2)若{b_n}为等比数列，b₁=a₂,b₂=a₃+2,求数列{b,}的公比q及前n项和T_n.

答 案：(1)所以a₆=19.则数列{an}的公差，通项公式为an=a₆+(n-6)d=19+4n-24=4n-5.(2)因为b1=a2=4×2-5=3,b2=a3+2=4×3-5+2=9,所以则

填空题

1、直线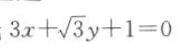的倾斜角是（）  

答 案：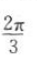

解 析：因为直线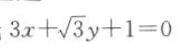的斜率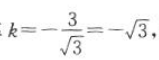所以该直线的倾斜角是

2、圆(x—2)²+(y+2)²=2截直线x-y-5=0所得的弦长为()  

答 案：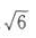

解 析：(x-2)²+(y+2)²=2的圆心为(2,一2),半径r=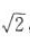,圆心到直线x-y-5=0的距离d=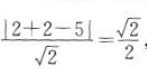,所以弦长为