2024年成考专升本《高等数学一》每日一练试题08月14日
考试问答
2024-08-14
11:37:10
收藏
单选题
1、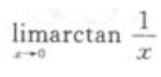 =()。
=()。
- A:
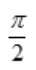
- B:-
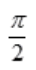
- C:±
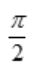
- D:不存在
答 案:D
解 析: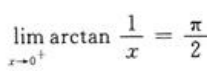 ,
, ,所以
,所以 不存在。
不存在。
2、函数y=f'(x)在点x0处可导是函数f(x)在点x0处连续的()。
- A:充分条件
- B:必要条件
- C:充分必要条件
- D:既非充分也非必要条件
答 案:A
解 析:函数y=f'(x)在点x0处可导,则必然在点x0处连续;但函数f(x)在点x0处连续,不一定得到函数在点x0处可导,所以函数y=f'(x)在点x0处可导是函数f(x)在点x0处连续的充分非必要条件。
3、当x→0时,x2-sinx是x的()。
- A:高阶无穷小
- B:等价无穷小
- C:同阶无穷小,但不是等价无穷小
- D:低阶无穷小
答 案:C
解 析: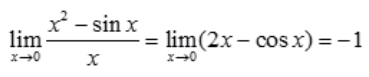 ,故x2-sinx是x的同阶无穷小,但不是等价无穷小。
,故x2-sinx是x的同阶无穷小,但不是等价无穷小。
主观题
1、求二元函数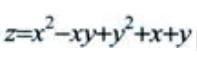 的极值。
的极值。
答 案:解: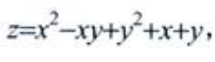 则由
则由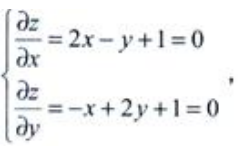
 点P(-1,1)为唯一驻点,
点P(-1,1)为唯一驻点,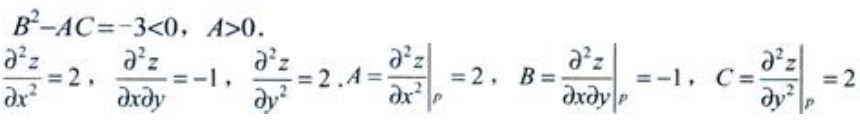 因此点(-1,-1)为z的极小值点,极小值为-1。
因此点(-1,-1)为z的极小值点,极小值为-1。
2、在曲线 上求一点M0,使得如图中阴影部分的面积S1与S2之和S最小。
上求一点M0,使得如图中阴影部分的面积S1与S2之和S最小。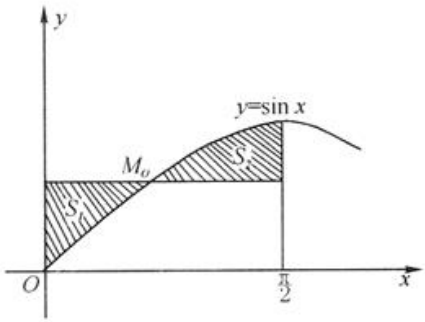
答 案:解:设点M0的横坐标为x0,则有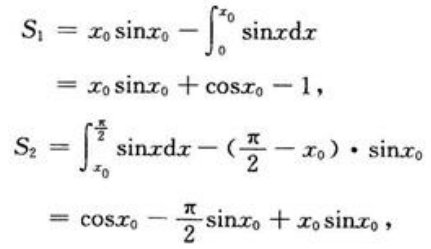 则
则 S为x0的函数,将上式对x0求导得
S为x0的函数,将上式对x0求导得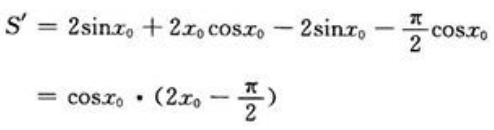 令S'=0,得
令S'=0,得 ,所以
,所以 由于只有唯一的驻点,所以
由于只有唯一的驻点,所以 则点M0的坐标为
则点M0的坐标为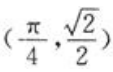 为所求。
为所求。
3、计算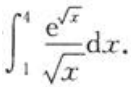
答 案:解:令t=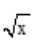 ,则x=t2,dx=2tdt。当x=1时,t=1;当x=4时。t=2。则
,则x=t2,dx=2tdt。当x=1时,t=1;当x=4时。t=2。则
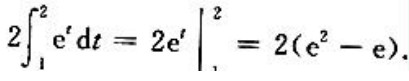
填空题
1、设f(x,y)与g(x,y)在区域D上连续,而且f(x,y)<g(x,y),则二重积分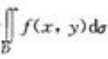 与
与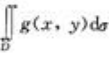 的大小关系是前者比后者()。
的大小关系是前者比后者()。
答 案:小
解 析:因为二重积分的几何意义是柱体的体积,故由f(x,y)<g(x,y)可知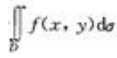 小于
小于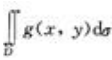 。
。
2、设z=exy,则dz=()
答 案:exy(ydx+xdy)
解 析: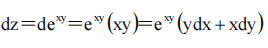
3、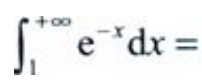 ()。
()。
答 案:e-1
解 析:所给积分为广义积分,因此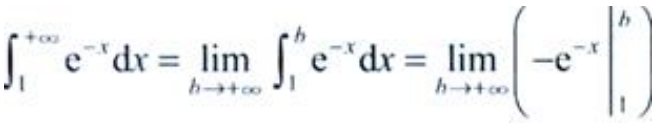
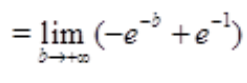
简答题
1、计算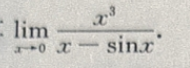
答 案: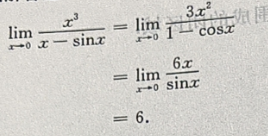
更多推荐

