2024年成考专升本《高等数学二》每日一练试题08月11日
考试问答
2024-08-11
11:21:37
收藏
判断题
1、若 ,则
,则 。()
。()
答 案:错
解 析: 所以
所以
单选题
1、 =().
=().
- A:0
- B:1
- C:
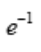
- D:+∞
答 案:C
解 析:因为在x=0处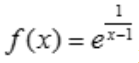 是连续的,所以
是连续的,所以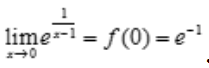 .
.
2、如果函数y=f(x)在x0处满足 ,则().
,则().
- A:x0是驻点
- B:x0不是驻点
- C:x0是极值点
- D:x0不是极值点
答 案:A
解 析:驻点的定义:函数的一阶导数为0的点的x的值,驻点可以划分函数的单调区间.可导函数f(x)的极值点一定是它的驻点;但反过来,函数的驻点不一定是极值点.例如函数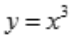 ,x=0是函数的驻点,但不是极值点.
,x=0是函数的驻点,但不是极值点.
主观题
1、计算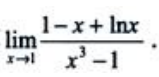
答 案:解:由洛必达法则得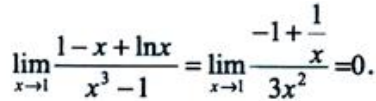
2、计算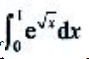 .
.
答 案:解:设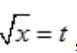 ,则dx=2tdt.当x=0时,t=0;当x=1时,t=1.则
,则dx=2tdt.当x=0时,t=0;当x=1时,t=1.则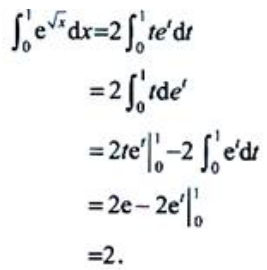
填空题
1、设y=3x2+ln3,则y'=()
答 案:6x
解 析: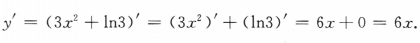
2、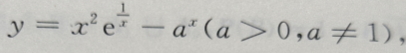 则y'=()
则y'=()
答 案: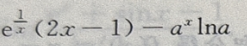
解 析: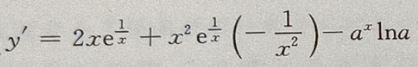

简答题
1、求函数 的单调区间、极值及函数曲线的凸凹性区间、拐点和渐近线.
的单调区间、极值及函数曲线的凸凹性区间、拐点和渐近线.
答 案:
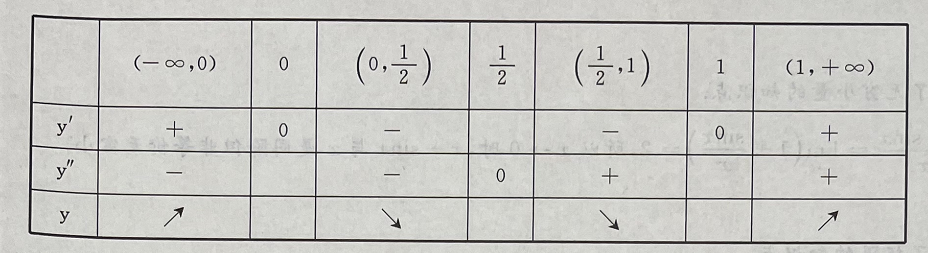 所以函数y的单调增区间为
所以函数y的单调增区间为 单调减区间为(0,1);函数y的凸区间为
单调减区间为(0,1);函数y的凸区间为 凹区间为
凹区间为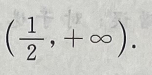 故x=0时,函数有极大值0,x=1时,函数有极小值-1,且点
故x=0时,函数有极大值0,x=1时,函数有极小值-1,且点 为拐点,因
为拐点,因 不存在,且
不存在,且 没有无意义的点,故函数没有渐近线。
没有无意义的点,故函数没有渐近线。
2、求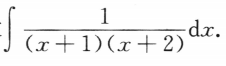
答 案: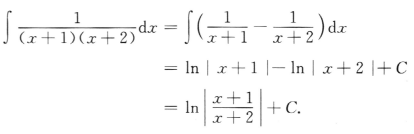
更多推荐

