单选题

1、级数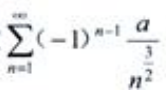（a为大于零的常数）（）。

• A：绝对收敛
• B：条件收敛
• C：发散
• D：收敛性与a有关

答 案：A

解 析：级数，因此为收敛级数，由级数性质可知绝对收敛。

2、下列方程中表示椭球面的是（）。

• A：x²＋y²－z²＝1
• B：x²－y²＝0
• C：
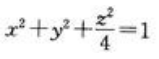
• D：x²＋y²＝z²

答 案：C

解 析：A项，双曲面的方程为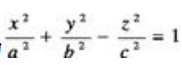，所以为双曲面；B项，x²－y²＝0表示两条垂直的直线；C项，椭球面的方程为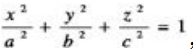，符合这一特征；D项，x²＋y²＝z²表示圆锥体。

3、（）。

• A：0
• B：
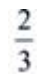
• C：1
• D：

答 案：A

解 析：当x→∞时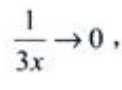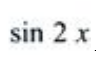，为有界函数，有界变量与无穷小之积为无穷小，故。

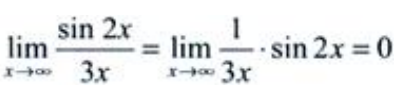主观题

1、求微分方程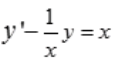的通解。

答 案：解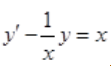：为一阶线性微分方程，则

2、求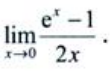

答 案：解：利用洛必达法则，得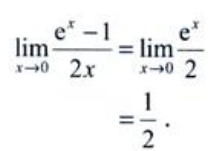

3、设e^x＋x＝e^y＋y，求。

答 案：解：对等式两边同时微分，得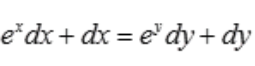，故。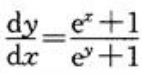

填空题

1、过点M（1，2，－1）且与平面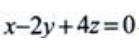垂直的直线方程为（）。

答 案：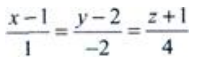

解 析：由于直线与平面x－2y＋4z＝0垂直，可取直线方向向量为（1，－2，4），因此所求直线方程为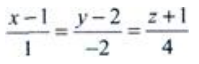

2、幂级数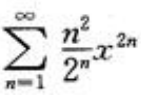的收敛半径是（）。

答 案：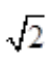

解 析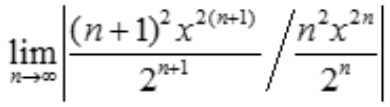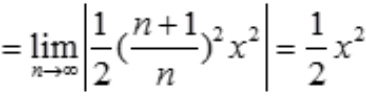：，当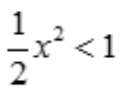时，级数收敛，故收敛区间为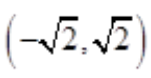，收敛半径。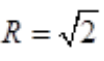

3、级数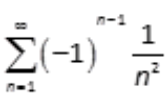（）收敛。

答 案：绝对

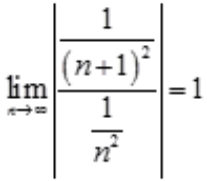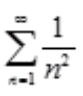解 析：因为，又级数收敛，所以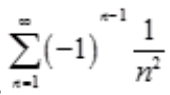绝对收敛。

简答题

1、求函数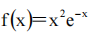的单调区间和极值.  

答 案： 由表可知，函数的单调曾区间为（0，2）；单调减区间为（-∞，0），（2，+∞） 极大值为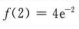，极小值为f（0）=0.