单选题

1、设M=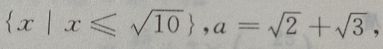那么（）

• A：
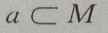
• B：
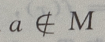
• C：
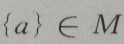
• D：

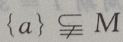
答 案：D

解 析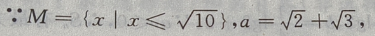： M是集合，a为元素，{a}为集合，元素与集合的关系是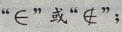集合与集合的关系是  

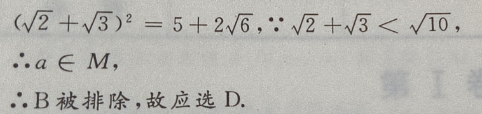
2、函数的图像与直线y=4的交点坐标为（）

• A：(0,4)
• B：(4,64)
• C：(1,4)
• D：(4,16)

答 案：C

解 析：令y=4^x=4，解得x=1，故所求交点为（1,4).

3、已知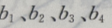成等差数列，且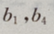为方程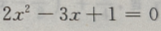的两个根，则的值为（）  

• A：
• B：
• C：
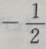
• D：

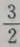
答 案：D

解 析：由根与系数的关系得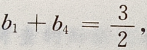由等差数列的性质得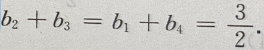

4、若函数y=f(x)在[-1,1]上是单调函数,则使得y=f(sinx)必为单调函数的区间是()  

• A：R
• B：[-1,1]
• C：
• D：[-sin1 ,sin1]

答 案：C

解 析：y=f(x)在[-1,1]上是单调函数,所以y=f(x)的单调区间为[-1,1]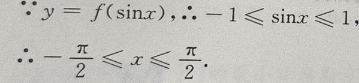  

主观题

1、已知直线l的斜率为1，l过抛物线C：的焦点，且与C交于A,B两点.
(I）求l与C的准线的交点坐标；
(II）求|AB|．

答 案：(I）C的焦点为，准线为由题意得l的方程为因此l与C的准线的交点坐标为(II）由得设A（x1,y1）.B（x2,y2），则因此

2、在△ABC中，AB=2，BC=3,B=60°，求AC及△ABC的面积

答 案：

3、设函数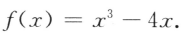
(I）求f'(2)；
(II）求f(x）在区间[一1,2]的最大值与最小值．

答 案：(I）因为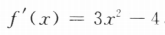，所以f'(2)=3×2²-4=8.(II）因为x＜-1，f(-1)=3.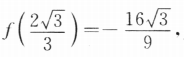f(2)=0.
所以f(x）在区间[一1,2]的最大值为3，最小值为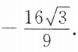

4、在△ABC中，B=120°,C=30°,BC=4，求△ABC的面积．

答 案：因为A= 180°-B-C=30°，所以AB = BC=4.因此△ABC的面积

填空题

1、过点（2，0）作圆x2+y2=1的切线，切点的横坐标为（）。

答 案：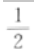

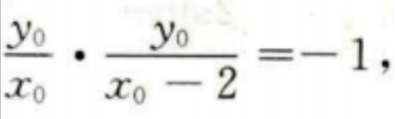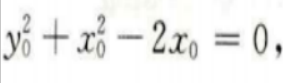
解 析：本题主要考查的知识点为圆的切线. 设切点(x0,y0)则有 即所以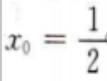故切点横坐标为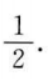  

2、函数y=-x²+ax图像的对称轴为x=2，则a=______。

答 案：4  

解 析：本题主要考查的知识点为二次函数的性质。 由题意，该函数图像的对称轴为得a=4。