2024年成考专升本《高等数学二》每日一练试题07月24日
考试问答
2024-07-24
11:29:04
收藏
判断题
1、若
，则
。（）
答 案：错
解 析：
所以
单选题
1、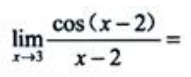
（）.
- A：1
- B：cos1
- C：0
- D：
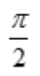
答 案：B
解 析：因为函数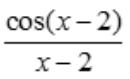
在x=3处连续，故
.
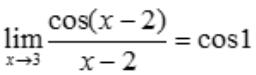2、设函数z＝x2y3，则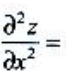
（）.
- A：2y3
- B：6xy2
- C：6y2
- D：12xy
答 案：A
解 析：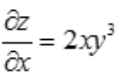
，
.
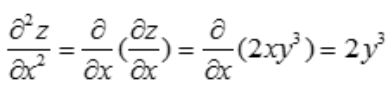主观题
1、设D为曲线y＝1－x2，直线y＝x＋1及x轴所围成的平面图形（如图所示）．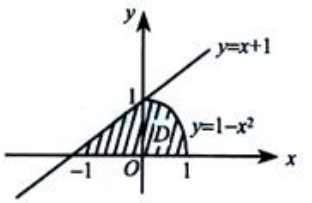
（1）求平面图形D的面积S；
（2）求平面图形D绕x轴旋转一周所成旋转体的体积Vx．
答 案：解：（1）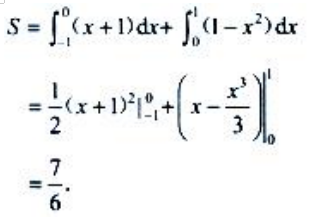
（2）
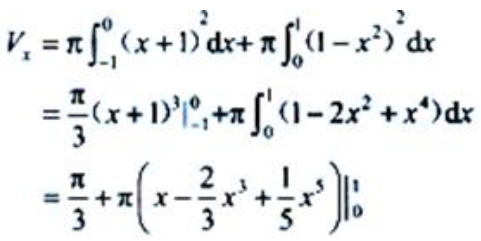
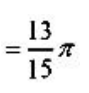
2、设函数y＝sinx2＋2x，求dy．
答 案：解：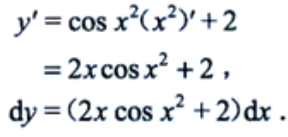
填空题
1、函数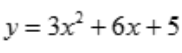
的单调减少区间是（）．
答 案：（－∞，－1）
解 析：函数的定义域为（－∞，＋∞）．令
，解得驻点ｘ＝－1．在区间（－∞，－1）内，y'＜0，函数单调减少；在区间（－1，＋∞）内，y'＞0，函数单调增加．
2、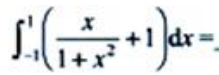
()．
答 案：2
解 析：积分区间关于原点对称，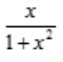
是奇函数，故
．
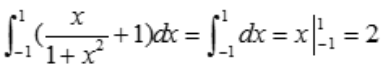简答题
1、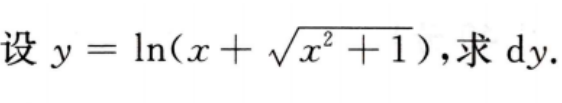
答 案：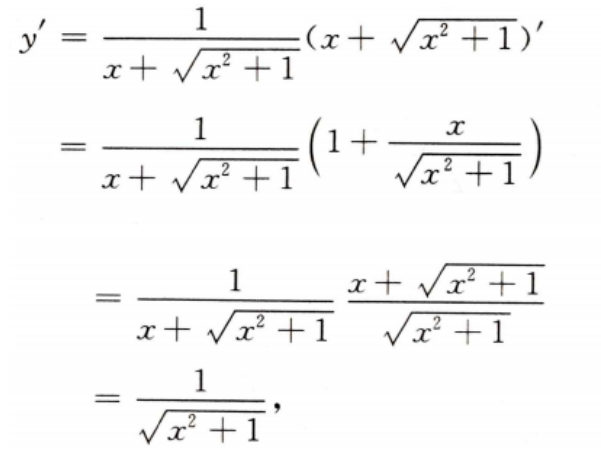
2、求函数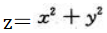
在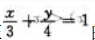
条件下的极值及极值点．
答 案：令
于是
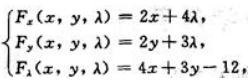求解方程组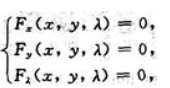
得其驻点
故点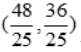
为极值点，且极值为
更多推荐
