2024年成考专升本《高等数学一》每日一练试题07月19日
考试问答
2024-07-19
11:37:58
收藏
单选题
1、设函数f(x)=3x3+ax+7在x=1处取得极值,则a=()
- A:9
- B:3
- C:-3
- D:-9
答 案:D
解 析:函数f(x)在x=1处取得极值,而f’(x)=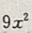 +a,故f’(1)=9+a=0,解得a=-9。
+a,故f’(1)=9+a=0,解得a=-9。
2、设y=e-x,则dy=()
- A:e-xdx
- B:-e-xdx
- C:exdx
- D:-exdx
答 案:B
解 析: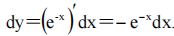
3、 ()。
()。
- A:ex
- B:e2
- C:e
- D:1
答 案:D
解 析:所求极限为“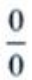 ”型,由洛必达法则可得
”型,由洛必达法则可得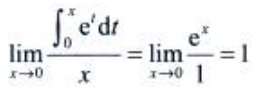 或先求出
或先求出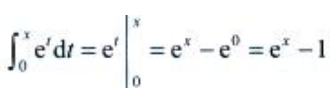 ,则
,则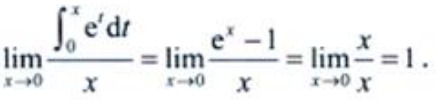
主观题
1、用围墙围成216m2的一块矩形场地,正中间用一堵墙将其隔成左右两块,此场地长和宽各为多少时建筑材料最省?
答 案:解:设宽为xm,则长为 m,围墙总长为
m,围墙总长为 ,
,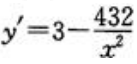 ,令y'=0,得x=±12,x=12不合题意舍去。所以x=12m是唯一驻点,而
,令y'=0,得x=±12,x=12不合题意舍去。所以x=12m是唯一驻点,而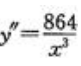 ,故
,故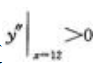 所以x=12m时y最小,即长为18m,宽为12m时建筑材料最省。
所以x=12m时y最小,即长为18m,宽为12m时建筑材料最省。
2、设y=xsinx,求y'。
答 案:解:y=xsinx,
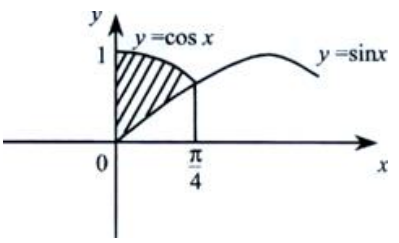
3、求曲线y=sinx、y=cosx、直线x=0在第一象限所围图形的面积A及该图形绕x轴旋转一周所得旋转体的体积Vx。
答 案:解:由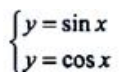 ,解得两曲线交点的x坐标为
,解得两曲线交点的x坐标为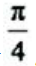 。
。
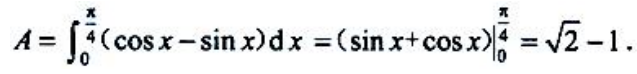

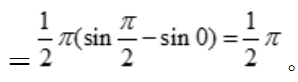
填空题
1、 =()。
=()。
答 案:5sinx+C
解 析: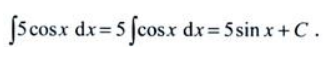
2、若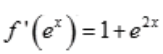 ,且f(0)=1,则f(x)=()。
,且f(0)=1,则f(x)=()。
答 案: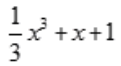
解 析: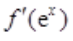 =1+e2x,等式两边对ex积分有
=1+e2x,等式两边对ex积分有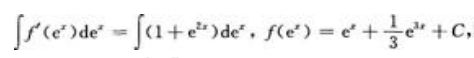
 所以
所以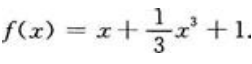
3、设z=xy,则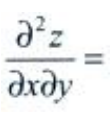 ()。
()。
答 案:1
解 析:z=xy,则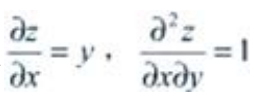 。
。
简答题
1、给定曲线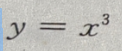 与直线y=px-q(其中p>0),求p与q为关系时,直线y=px-q
与直线y=px-q(其中p>0),求p与q为关系时,直线y=px-q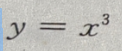 的切线。
的切线。
答 案:由题意知,再切点处有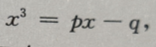 两边对x求导得
两边对x求导得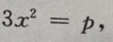

更多推荐

